128 64 32 16 8 4 2 1
arrobajuarez
Nov 07, 2025 · 10 min read
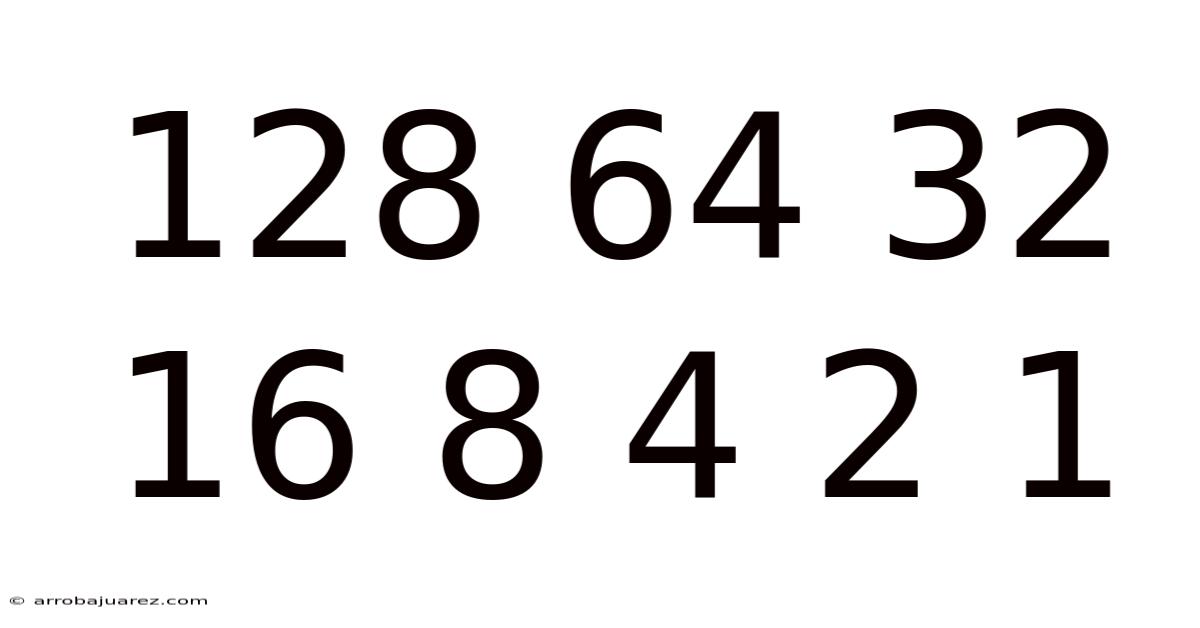
Table of Contents
128 64 32 16 8 4 2 1: Unveiling the Power of Binary Representation
The sequence 128, 64, 32, 16, 8, 4, 2, 1 is more than just a series of descending numbers; it's a fundamental cornerstone of computer science and digital technology. This sequence represents the place values in an 8-bit binary number system, forming the very basis of how computers store, process, and transmit information. Understanding this sequence unlocks the door to comprehending the intricate world of binary code and its pervasive influence on our digital lives.
The Foundation: Decimal vs. Binary
To truly appreciate the significance of 128, 64, 32, 16, 8, 4, 2, 1, we must first differentiate between the decimal system (base-10) that we use daily and the binary system (base-2) employed by computers.
-
Decimal System (Base-10): This system utilizes ten digits (0-9) to represent numbers. Each position in a decimal number represents a power of 10. For instance, the number 345 is interpreted as (3 * 10^2) + (4 * 10^1) + (5 * 10^0) = 300 + 40 + 5.
-
Binary System (Base-2): This system only uses two digits: 0 and 1. Each position in a binary number represents a power of 2. The sequence 128, 64, 32, 16, 8, 4, 2, 1 precisely represents these powers of 2:
- 128 = 2^7
- 64 = 2^6
- 32 = 2^5
- 16 = 2^4
- 8 = 2^3
- 4 = 2^2
- 2 = 2^1
- 1 = 2^0
Decoding the 128 64 32 16 8 4 2 1 Sequence: An 8-Bit Deep Dive
The sequence 128 64 32 16 8 4 2 1 corresponds to the place values within an 8-bit binary number. An "8-bit" system means that each number is represented using eight binary digits (bits). Each bit can be either a 0 or a 1. The position of each bit, from right to left, corresponds to a value in our sequence.
Let's visualize this:
Bit Position: 7 6 5 4 3 2 1 0
Place Value: 128 64 32 16 8 4 2 1
To convert a binary number to its decimal equivalent, you multiply each bit by its corresponding place value and then sum the results.
Example 1: Converting the binary number 01010101 to decimal.
Binary: 0 1 0 1 0 1 0 1
Place Value: 128 64 32 16 8 4 2 1
Calculation: (0*128) + (1*64) + (0*32) + (1*16) + (0*8) + (1*4) + (0*2) + (1*1) = 0 + 64 + 0 + 16 + 0 + 4 + 0 + 1 = 85
Therefore, the binary number 01010101 is equivalent to the decimal number 85.
Example 2: Converting the binary number 11111111 to decimal.
Binary: 1 1 1 1 1 1 1 1
Place Value: 128 64 32 16 8 4 2 1
Calculation: (1*128) + (1*64) + (1*32) + (1*16) + (1*8) + (1*4) + (1*2) + (1*1) = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Therefore, the binary number 11111111 is equivalent to the decimal number 255. This is the highest possible value representable by an 8-bit number.
Example 3: Converting the binary number 00000000 to decimal.
Binary: 0 0 0 0 0 0 0 0
Place Value: 128 64 32 16 8 4 2 1
Calculation: (0*128) + (0*64) + (0*32) + (0*16) + (0*8) + (0*4) + (0*2) + (0*1) = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
Therefore, the binary number 00000000 is equivalent to the decimal number 0.
Converting Decimal to Binary: The Reverse Process
The process can also be reversed to convert a decimal number into its binary equivalent. This involves repeatedly dividing the decimal number by 2 and recording the remainders. The remainders, read in reverse order, form the binary representation.
Example: Converting the decimal number 42 to binary.
- 42 / 2 = 21, Remainder = 0
- 21 / 2 = 10, Remainder = 1
- 10 / 2 = 5, Remainder = 0
- 5 / 2 = 2, Remainder = 1
- 2 / 2 = 1, Remainder = 0
- 1 / 2 = 0, Remainder = 1
Reading the remainders in reverse order, we get 101010. Therefore, the decimal number 42 is equivalent to the binary number 101010. To represent this as a full 8-bit number, we pad it with leading zeros: 00101010.
Here's a tabular representation of the process:
| Division | Quotient | Remainder |
|---|---|---|
| 42 / 2 | 21 | 0 |
| 21 / 2 | 10 | 1 |
| 10 / 2 | 5 | 0 |
| 5 / 2 | 2 | 1 |
| 2 / 2 | 1 | 0 |
| 1 / 2 | 0 | 1 |
Binary equivalent: 101010 (or 00101010 as an 8-bit number).
Why Binary? The Computer's Language
Computers operate using electricity. The presence or absence of an electrical signal can be easily represented by two states: ON or OFF. These states are naturally mapped to the binary digits 1 and 0, respectively. This makes binary the most efficient and reliable way for computers to represent and process information.
Here's a breakdown of the advantages of using binary in computers:
- Simplicity: Binary requires only two states, making circuit design simpler and more reliable.
- Reliability: Distinguishing between two states (ON/OFF) is less prone to errors than distinguishing between ten states (as in the decimal system).
- Cost-Effectiveness: Simpler circuits translate to lower manufacturing costs.
- Logic Operations: Binary lends itself naturally to Boolean logic, which is essential for performing calculations and making decisions within a computer.
Beyond 8-Bit: Scaling Up to Larger Numbers
While the sequence 128 64 32 16 8 4 2 1 helps understand the fundamentals of 8-bit binary representation, modern computers use larger bit systems like 16-bit, 32-bit, and 64-bit. These larger systems allow for the representation of much larger numbers and more complex data.
The concept remains the same: each bit position represents a power of 2. For example, in a 16-bit system, the place values would extend beyond 128:
2^15, 2^14, 2^13, 2^12, 2^11, 2^10, 2^9, 2^8, 2^7, 2^6, 2^5, 2^4, 2^3, 2^2, 2^1, 2^0
Which translates to:
32768, 16384, 8192, 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1
The maximum value that can be represented by a 16-bit number is 65535 (2^16 - 1). Similarly, a 32-bit system can represent numbers up to 4,294,967,295 (2^32 - 1), and a 64-bit system can represent incredibly large numbers, making them suitable for demanding applications like scientific computing and large databases.
Applications of Binary in Computer Science
The binary system, underpinned by the sequence 128 64 32 16 8 4 2 1 and its extensions, is the bedrock of numerous applications within computer science:
- Data Storage: All types of data, including text, images, audio, and video, are ultimately stored as binary code on storage devices like hard drives and solid-state drives.
- Data Transmission: Data transmitted over networks, including the internet, is encoded in binary format.
- Computer Architecture: The central processing unit (CPU) of a computer operates on binary instructions to perform calculations and control the system.
- Programming Languages: While programmers typically write code in high-level languages, these languages are eventually translated into machine code (binary instructions) that the computer can execute.
- Networking: Network protocols rely on binary representation for addressing, routing, and error detection.
- Digital Electronics: Binary logic is fundamental to the design and operation of digital circuits.
- Image Processing: Images are represented as arrays of pixels, with each pixel's color value encoded in binary.
- Cryptography: Encryption algorithms rely heavily on binary operations to secure data.
Representing Characters: ASCII and Unicode
Binary isn't just for numbers; it's also used to represent characters, symbols, and instructions. Two of the most prominent character encoding standards are ASCII and Unicode.
-
ASCII (American Standard Code for Information Interchange): ASCII uses 7 bits to represent 128 characters, including uppercase and lowercase letters, numbers, punctuation marks, and control characters. An extended version uses 8 bits, allowing for 256 characters. The sequence 128 64 32 16 8 4 2 1 is directly relevant to understanding how ASCII characters are represented in binary. For example, the letter "A" is represented by the decimal number 65, which corresponds to the binary code 01000001.
-
Unicode: Unicode is a more comprehensive character encoding standard that uses a variable number of bits (typically 16 or 32) to represent a much wider range of characters, including characters from different languages and special symbols. Unicode is essential for supporting multilingual content and ensuring consistent character representation across different platforms. While the basic principles of binary representation still apply, Unicode employs more complex encoding schemes.
Logic Gates and Boolean Algebra
The binary system is intrinsically linked to Boolean algebra, a branch of mathematics that deals with logical operations on binary variables (0 and 1). These logical operations are implemented in computers using logic gates, which are electronic circuits that perform basic logical functions.
Common logic gates include:
- AND Gate: The output is 1 only if both inputs are 1.
- OR Gate: The output is 1 if at least one input is 1.
- NOT Gate: The output is the inverse of the input (1 becomes 0, and 0 becomes 1).
- XOR Gate: The output is 1 if the inputs are different (one is 0 and the other is 1).
These logic gates are combined to create more complex circuits that perform arithmetic operations, control data flow, and implement decision-making logic within a computer. The underlying principle is that everything is ultimately based on binary values and logical operations performed on those values.
Common Misconceptions
-
Binary is Difficult: While it may seem intimidating at first, the basic concepts of binary are relatively simple to grasp. Understanding the place values represented by the sequence 128 64 32 16 8 4 2 1 is the key.
-
Only Programmers Need to Know Binary: While programmers certainly benefit from a strong understanding of binary, it's also valuable for anyone working with computers or digital technology. A basic understanding of binary can help you troubleshoot problems, optimize performance, and gain a deeper appreciation for how computers work.
-
Binary is Outdated: Despite the advancements in computer technology, binary remains the fundamental language of computers. While higher-level abstractions are used to simplify programming and development, everything ultimately boils down to binary at the hardware level.
Conclusion
The sequence 128 64 32 16 8 4 2 1 is a gateway to understanding the core principles of computer science. It represents the place values in an 8-bit binary number system, which is the foundation for how computers store, process, and transmit information. By understanding this sequence, you gain a deeper appreciation for the digital world around us and the ingenious ways in which computers manipulate information. From representing numbers and characters to performing logical operations, binary is the silent language that powers our modern digital age. Embracing this understanding unlocks a world of possibilities for innovation and problem-solving in the ever-evolving landscape of technology. So, the next time you encounter the numbers 128, 64, 32, 16, 8, 4, 2, and 1, remember that they represent more than just a descending order; they represent the language of computers and the building blocks of our digital reality.
Latest Posts
Latest Posts
-
Use The Given Information To Find A
Nov 07, 2025
-
When Workers May Be Exposed To
Nov 07, 2025
-
Record The Entry To Close The Dividends Account
Nov 07, 2025
-
The Graph Of A Linear Function F Is Given
Nov 07, 2025
-
Which Of The Following Is An Example Of Homeostasis
Nov 07, 2025
Related Post
Thank you for visiting our website which covers about 128 64 32 16 8 4 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.