2 2x 2 X 12 0
arrobajuarez
Nov 05, 2025 · 11 min read
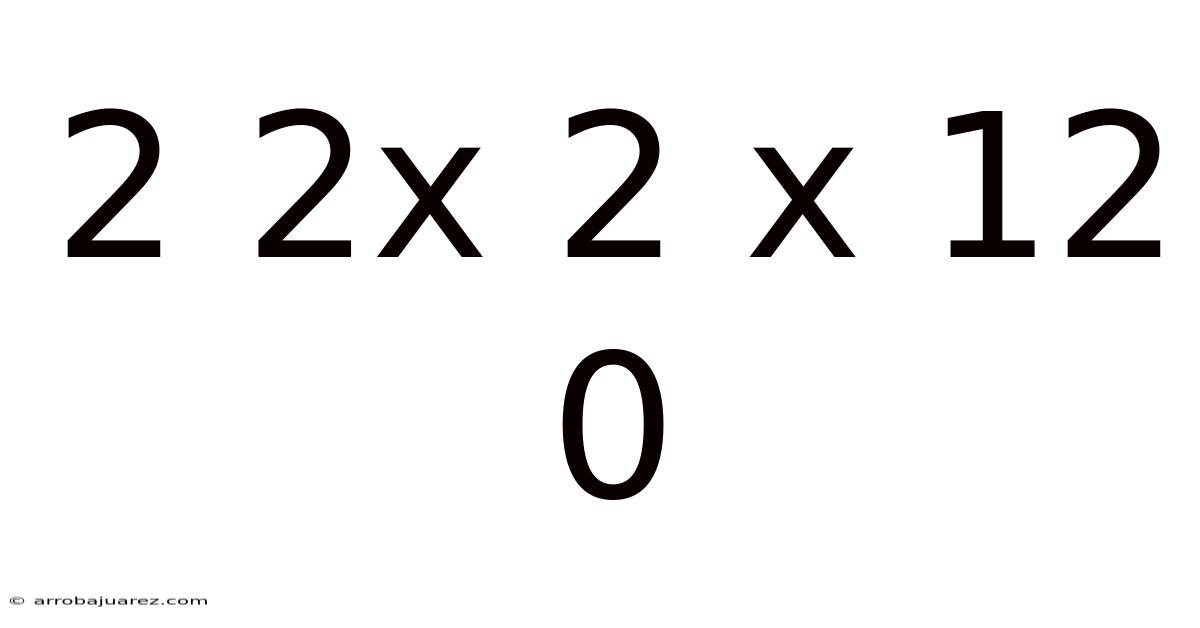
Table of Contents
Decoding the Enigma: Understanding "2 2x 2 x 12 0"
The sequence "2 2x 2 x 12 0" appears cryptic at first glance, sparking curiosity and potentially even a bit of mathematical anxiety. However, by dissecting this expression and exploring different interpretations, we can uncover its meaning and purpose. This exploration isn't just about finding a single answer; it's about understanding the nuances of mathematical notation, the importance of context, and the versatility of numbers. We'll delve into potential mathematical operations, explore its relevance in diverse fields, and ultimately, shed light on the possible intentions behind this seemingly enigmatic expression.
Unpacking the Components
Before attempting to solve or interpret "2 2x 2 x 12 0," it's crucial to understand each of its components:
- Numbers (2, 12, 0): These are the fundamental building blocks, representing numerical values.
- x: This symbol is generally interpreted as the multiplication operator in mathematics.
- Absence of Operators: The spaces between the numbers and the 'x' symbols can create ambiguity, which is something we will need to address.
The real challenge lies in deciphering the intended operations and the order in which they should be applied. This requires us to consider different possible interpretations.
Possible Interpretations & Solutions
Several interpretations of "2 2x 2 x 12 0" are possible, each leading to a different result. Let's explore the most likely ones:
1. Standard Multiplication:
This is the most straightforward interpretation, assuming that all 'x' symbols represent multiplication. In this case, the expression would be:
2 * 2 * 2 * 120
Calculation:
- 2 * 2 = 4
- 4 * 2 = 8
- 8 * 120 = 960
Therefore, the result would be 960.
2. Order of Operations (PEMDAS/BODMAS):
While the expression primarily involves multiplication, it's essential to remember the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). In this case, since we only have multiplication, we proceed from left to right, which is what we already did in interpretation 1. This interpretation still yields 960.
3. Exponentiation and Multiplication:
The "2x" could potentially be interpreted as an exponent. If we assume that "2x" means "2 to the power of," then the expression could be rewritten as:
2 2^2 * 120
Calculation:
- 2^2 = 4
- 2 * 4 = 8
- 8 * 120 = 960
Surprisingly, even with exponentiation, the final result is still 960 in this specific case because only 2 to the power of 2 is there in the sequence.
4. String Concatenation (Less Likely in a Mathematical Context):
In some programming contexts, the absence of an operator might imply string concatenation (joining strings together). However, this is less likely in a purely mathematical scenario. If we were to treat the numbers as strings and concatenate them, we would get:
"222120"
This is a very different outcome and unlikely to be the intended meaning in a mathematical setting.
5. Misinterpretation or Typographical Error:
It's also possible that the expression contains a typographical error. Perhaps a different operator was intended (e.g., addition, subtraction, division), or a number was mistyped. Without additional context, it's difficult to determine if this is the case. For instance, if there was a + between 2 and 2x, then the whole result would change.
6. Function Notation:
The expression could represent a function call or a sequence of operations within a specific defined function. If 'x' is not multiplication but part of a function name. However, without knowing the function, it's impossible to evaluate this.
7. Base Conversion or Representation:
Although less likely, “2 2x 2 x 12 0” could be a representation in a non-decimal number system. The ‘x’ could represent a digit in a given base, or it might imply a transformation or conversion from one base to another.
The Most Plausible Solution
Based on the standard conventions of mathematical notation, the most plausible interpretation of "2 2x 2 x 12 0" is simple multiplication. Therefore, the solution is 960.
Why the Ambiguity Matters
The ambiguity surrounding this expression highlights the importance of clear and precise mathematical notation. In formal mathematics, expressions are carefully constructed to avoid any potential misinterpretations. When working with less formal expressions, it's crucial to consider the context and make reasonable assumptions based on common mathematical practices. This situation underscores why mathematical communication prioritizes rigor and detail. Ambiguity can lead to errors, misunderstandings, and ultimately, incorrect results.
Applications and Relevance
While "2 2x 2 x 12 0" in itself might seem like a simple exercise, the underlying concepts of mathematical operations and interpretation have broad applications across various fields:
- Computer Science: Programming languages rely heavily on precise mathematical notation. Understanding operator precedence, data types, and function calls is essential for writing correct and efficient code. The interpretation of symbols and the order in which operations are performed are fundamental to how computers process information.
- Engineering: Engineers use mathematical models to design and analyze systems. Accurate calculations are crucial for ensuring the safety and reliability of these systems. From calculating stress and strain in structures to modeling fluid flow in pipelines, engineers constantly manipulate mathematical expressions.
- Finance: Financial analysts use mathematical models to assess risk, predict market trends, and manage investments. A clear understanding of mathematical operations is vital for making informed financial decisions. Compound interest calculations, statistical analysis of market data, and portfolio optimization all depend on a solid grasp of mathematical principles.
- Data Science: Data scientists use statistical methods and machine learning algorithms to extract insights from data. These methods often involve complex mathematical calculations. Understanding linear algebra, calculus, and probability is essential for developing and interpreting machine learning models.
- Cryptography: Cryptography relies on mathematical algorithms to encrypt and decrypt sensitive information. The security of these algorithms depends on the difficulty of solving certain mathematical problems. Number theory, abstract algebra, and computational complexity are all important areas of mathematics in the field of cryptography.
In all these fields, the ability to interpret and manipulate mathematical expressions accurately is paramount. The exercise of deciphering "2 2x 2 x 12 0" serves as a reminder of the importance of precision and clarity in mathematical communication.
Building a Mental Toolkit for Problem Solving
Decoding expressions like "2 2x 2 x 12 0" encourages us to develop a mental toolkit for problem-solving:
- Break it Down: Deconstruct the problem into smaller, manageable parts. Identify the individual components (numbers, operators, symbols).
- Consider Multiple Interpretations: Explore different possible meanings of the expression. Don't settle for the first interpretation that comes to mind.
- Apply the Rules: Use your knowledge of mathematical rules and conventions (order of operations, notation) to evaluate each interpretation.
- Look for Context: If possible, consider the context in which the expression appears. This can provide clues about the intended meaning.
- Check for Errors: Be aware that the expression might contain errors (typos, incorrect notation).
- Simplify: If the expression is complex, try to simplify it by performing intermediate calculations or rewriting it in a different form.
- Test Your Solution: Once you have a solution, test it to see if it makes sense in the context of the problem.
- Be Open to Revision: If your initial solution doesn't seem right, be prepared to revise your approach and try a different interpretation.
This problem-solving approach is applicable not only to mathematical problems but also to a wide range of challenges in other fields.
The Beauty of Mathematical Exploration
Even a seemingly simple expression like "2 2x 2 x 12 0" can lead to a fascinating exploration of mathematical concepts. It highlights the importance of clarity, precision, and critical thinking in mathematics. By considering different interpretations and applying our knowledge of mathematical rules, we can arrive at a plausible solution. This exercise also demonstrates the versatility of mathematics and its relevance to various fields. Mathematical exploration isn't just about finding the right answer; it's about developing a deeper understanding of the language of numbers and its power to describe the world around us. The beauty of mathematics lies in its ability to reveal hidden patterns, solve complex problems, and provide a framework for understanding the universe.
Addressing Potential Misconceptions
It’s vital to acknowledge potential misconceptions that might arise when interpreting expressions like this. Some individuals might instinctively apply unconventional operations or overlook the standard order of operations. Reinforcing the fundamentals of mathematical notation and order of operations is key to preventing these errors. Stressing the significance of context and the potential for typographical errors also helps cultivate a more nuanced understanding.
The Role of Technology
Modern calculators and computer algebra systems (CAS) can effortlessly evaluate mathematical expressions, but they operate based on programmed rules and assumptions. While technology can expedite calculations, it's crucial to comprehend the underlying mathematical principles. Relying solely on technology without understanding the fundamentals can lead to misinterpretations and errors. Technology should serve as a tool to enhance understanding, not as a replacement for it. Using technology to verify solutions and explore different interpretations can be a valuable learning experience.
Implications for Education
This exploration has significant implications for mathematics education. It underscores the need to emphasize conceptual understanding alongside procedural fluency. Students should be encouraged to think critically about mathematical expressions, explore different interpretations, and justify their reasoning. Rote memorization of rules is insufficient; students need to develop a deep understanding of the underlying concepts. Incorporating open-ended problems that require students to interpret and analyze mathematical expressions can foster critical thinking skills and enhance mathematical literacy. Furthermore, connecting mathematical concepts to real-world applications can make learning more engaging and relevant.
The Iterative Nature of Problem Solving
Solving "2 2x 2 x 12 0" may seem straightforward upon first glance, but the real value comes from considering alternative interpretations. This highlights the iterative nature of problem-solving. Initially, assumptions may be made based on incomplete information, leading to a preliminary solution. However, as one explores different possibilities and gathers more context, the solution can be refined and improved. This iterative process is fundamental to scientific inquiry, engineering design, and many other fields.
Concluding Thoughts
The journey through "2 2x 2 x 12 0" demonstrates that even a simple-looking expression can harbor complexities and spark insightful discussions. While the most probable answer is 960, the real takeaway is the process of exploration, critical thinking, and the appreciation of mathematical nuance. Mathematical literacy involves not just calculating answers but also interpreting, analyzing, and communicating mathematical ideas effectively. The ability to decode and make sense of quantitative information is increasingly important in today's data-driven world. By embracing the challenges and ambiguities that arise in mathematics, we can cultivate a deeper understanding and appreciation for the power and beauty of this fundamental discipline.
FAQ: Decoding "2 2x 2 x 12 0"
Q: What is the most likely answer to "2 2x 2 x 12 0"?
A: The most likely answer, assuming standard mathematical notation, is 960. This is based on interpreting "x" as multiplication.
Q: Are there other possible answers?
A: Yes, there are other possible interpretations, but they are less likely without additional context. These include exponentiation, string concatenation (less likely), or a typographical error.
Q: Why is the expression ambiguous?
A: The ambiguity arises from the absence of clear operators between the numbers and the "x" symbol. This can lead to different interpretations.
Q: What does "PEMDAS/BODMAS" mean?
A: PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are acronyms that describe the order of operations in mathematics. They dictate the sequence in which operations should be performed to evaluate an expression correctly.
Q: Why is understanding mathematical notation important?
A: Understanding mathematical notation is crucial for clear communication, accurate calculations, and avoiding misinterpretations. It ensures that everyone interprets expressions in the same way.
Q: How can I improve my mathematical problem-solving skills?
A: You can improve your problem-solving skills by practicing regularly, understanding the underlying concepts, considering multiple interpretations, and breaking down problems into smaller parts.
Q: Can technology help solve mathematical problems?
A: Yes, technology like calculators and computer algebra systems can help solve mathematical problems, but it's crucial to understand the underlying mathematical principles. Technology should be used as a tool to enhance understanding, not as a replacement for it.
Q: What fields use mathematical concepts?
A: Mathematical concepts are used in a wide range of fields, including computer science, engineering, finance, data science, and cryptography.
Q: What should I do if I encounter a mathematical expression that I don't understand?
A: If you encounter an expression you don't understand, break it down into smaller parts, look for context, consider multiple interpretations, and consult resources like textbooks or online tutorials. Don't be afraid to ask for help from teachers or peers.
Q: How does this example relate to real-world problem-solving?
A: This example illustrates the importance of critical thinking, attention to detail, and the ability to consider multiple perspectives when solving problems. These skills are valuable in many areas of life, not just mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 2x 2 X 12 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.