2s 2 S 2 2s 5
arrobajuarez
Nov 18, 2025 · 11 min read
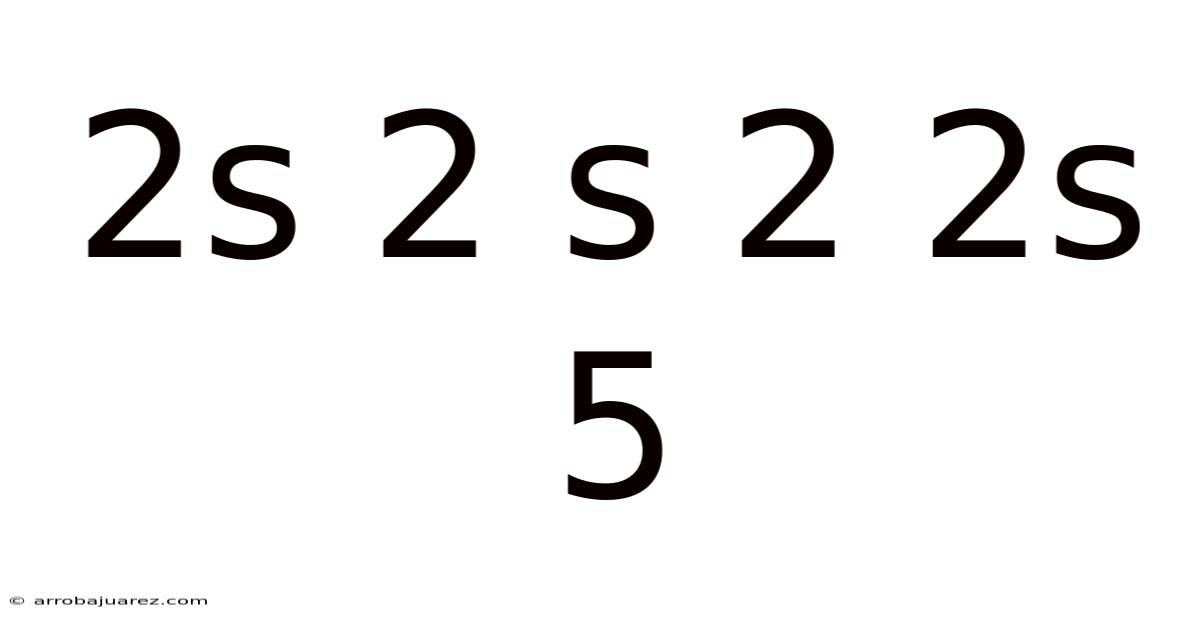
Table of Contents
The Enigmatic Sequence: Unraveling the Meaning of 2s 2 s 2 2s 5
The sequence "2s 2 s 2 2s 5" might seem like a random string of characters at first glance. However, within this seemingly simple arrangement lies a wealth of information, particularly relevant in fields like computer science, mathematics, music theory, and even genetics. This article will delve into the various interpretations and applications of this sequence, shedding light on its significance in different contexts. We will explore the sequence from the perspectives of programming, where it might represent array manipulation or memory allocation, to musical composition, where it could signify note durations or rhythmic patterns. We'll also consider its potential relevance in mathematical series and its less obvious connection to biological sequences. By dissecting "2s 2 s 2 2s 5," we aim to demonstrate how a seemingly simple code can hold complex meanings across disciplines.
Decoding "2s 2 s 2 2s 5" in Computer Science
In the realm of computer science, the interpretation of "2s 2 s 2 2s 5" hinges on the specific programming language or system being used. However, a few common interpretations emerge:
-
Array Indexing and Manipulation: "2s" might represent the index of an element within an array. The 's' could signify "second" or "string", indicating that we are dealing with the second element (index 1, remembering that indexing often starts at 0) of a data structure. The sequence could then represent a series of operations performed on array elements. For example, in Python-like pseudocode:
array = ["apple", "banana", "cherry", "date", "fig"] print(array[1]) # "banana" - The first "2s" print(array[1]) # "banana" - The second "2s" print(array[1]) # "banana" - The third "2s" print(array[1]) # "banana" - The fourth "2s" print(array[4]) # "fig" - The "5"This implies accessing the second element ("banana") four times, followed by accessing the fifth element ("fig"). This kind of repetition and then a change in index can be used for data manipulation, conditional processing, or even error checking within a larger program.
-
Memory Allocation and Addressing: In lower-level programming (like C or assembly), "2s" could be a symbolic representation of a memory address offset. The 's' could represent 'short' or 'segment'. Let's say each "2s" signifies an offset of two bytes within a memory block. The '5' could represent a final offset of five bytes. This could be used to access different parts of a data structure or to perform specific operations on different memory locations.
-
Instruction Sequencing: In assembly language, each component could represent a simplified instruction or a step in a process. For instance:
- "2s": Load the value from register 2 into a temporary register.
- "5": Store the value from the temporary register into memory location 5.
Therefore, the sequence could represent a series of load and store operations, crucial for data movement and computation within the CPU.
-
Regular Expressions (Regex) and String Matching: While less direct, one could interpret "2s" in the context of regular expressions. It could literally be searching for the character sequence "2s" within a larger string. The "5" could either be another search term or, more likely, indicate the number of occurrences or a condition related to the found sequences.
For example, if we were looking for patterns in a text, "2s 2 s 2 2s 5" could mean: "Find '2s' four times, and the overall matching sequence should be five characters long." This is a less common, but a potentially valid, interpretation depending on the specific regex engine and search parameters.
-
Data Serialization and Transmission: In networking or data storage, "2s" and "5" could represent specific data packets or segments being transmitted or stored. The 's' could denote a specific type of packet. Imagine a scenario where:
- "2s" signifies a control packet indicating a specific operation.
- "5" represents a data packet containing actual information.
The sequence then depicts the order in which these packets are processed or transmitted. This is a basic representation of protocol design.
Mathematical Interpretations of the Sequence
While seemingly simple, "2s 2 s 2 2s 5" can be interpreted within a mathematical framework in several ways:
-
Sequence Generation: We can consider this as the first few terms of a sequence and attempt to define a rule for generating subsequent terms. There's no single correct answer, and many functions could produce these initial values. One example could involve modulo arithmetic or a piece-wise defined function.
For instance, consider a function
f(n):- If
nis 1, 2, 3 or 4,f(n)= "2s" - If
nis 5,f(n)= "5"
While simple, this demonstrates the concept of defining a sequence based on given initial terms. More complex functions (polynomials, trigonometric functions with specific ranges) could also be used to generate the sequence.
- If
-
Symbolic Representation: The sequence could represent a series of operations or transformations applied to a starting value. Let's assign arbitrary numerical values to '2s' and '5'. For instance, let "2s" = 3 and "5" = 5. Then the sequence becomes 3, 3, 3, 3, 5. This now resembles a standard numerical sequence upon which mathematical operations can be applied (summation, finding the mean, etc.).
-
Modular Arithmetic: In modular arithmetic, we're concerned with the remainders after division. The sequence could represent remainders obtained after performing a series of calculations.
Let's consider modulo 7:
- If "2s" represents the number 9, then 9 mod 7 = 2. So, "2s" (or 9) mod 7 is equivalent to 2.
- And, 5 mod 7 = 5
While not directly "2s" but an element close to it, this illustrates how the sequence elements could be related via modular arithmetic. Determining the base number and the modulus would be necessary to decode the specific meaning in this scenario.
-
Game Theory: The sequence could represent a series of moves in a game. Each element ("2s" or "5") could correspond to a specific action that a player takes. The order matters and would influence the outcome of the game. This could be applied to simple games like tic-tac-toe or more complex games.
Musical Interpretations: Rhythm and Notation
The sequence "2s 2 s 2 2s 5" also lends itself to interpretation within music theory:
-
Note Durations and Rhythm: Each element could represent the duration of a musical note or rest. The 's' might stand for 'short' or 'sustained'.
- "2s" could represent a note of duration two units where 's' means shortened. Perhaps the note's full value is 1 beat, and 's' signifies a slight shortening or staccato effect.
- "5" could represent a note with a duration of five units (perhaps 2.5 beats if "2s" represents 1 beat).
Therefore, the sequence would represent a rhythmic pattern composed of four relatively short notes followed by a longer note. The specific duration of the "unit" would determine the overall tempo of the pattern.
-
Pitch and Intervals: While less direct, the numbers could be mapped to musical pitches within a scale. For example, in the C major scale:
- 2 could represent the note D.
- 5 could represent the note G.
The 's' could indicate a modification to the pitch, like a sharp (#) or flat (b). Thus, "2s" could represent D sharp. The sequence would then be a series of notes: D#, D#, D#, D#, G.
-
Chord Progressions: More abstractly, "2s" and "5" could represent different chords. The sequence would then represent a chord progression, like:
- "2s" = D minor chord (Dm)
- "5" = G major chord (G)
The sequence would then be: Dm, Dm, Dm, Dm, G. This is a common chord progression in various musical styles.
-
Time Signatures and Rhythmic Groupings: While less direct, "2s" could allude to compound time signatures, where beats are subdivided into three equal parts. If we consider the 's' as an abbreviation for swung rhythm, then 2/4 swung could be associated with '2s'. The "5" could indicate a measure with an unusual or irregular number of beats.
Biological Sequences: A Stretch, But Possible
It's more challenging to directly relate "2s 2 s 2 2s 5" to biological sequences, but not entirely impossible with some abstract mapping:
-
Amino Acid Sequences: In protein sequences, each letter represents an amino acid. We could arbitrarily assign:
- "2s" to represent the amino acid Alanine (Ala).
- "5" to represent the amino acid Glutamine (Gln).
The sequence then translates to a short peptide: Ala-Ala-Ala-Ala-Gln. While unlikely to have a specific, known function without further context, this demonstrates how a non-biological sequence could be mapped to a biological one. The 's' might represent some post-translational modification of Alanine, making it a unique variant.
-
DNA/RNA Representation: Similarly, we could map the elements to nucleotides in DNA or RNA:
- "2s" to Adenine (A)
- "5" to Cytosine (C)
The sequence becomes: A-A-A-A-C. This could represent a short DNA sequence, but again, its biological significance would depend on its context within a larger genome.
-
Gene Expression Levels: Imagine "2s" represents a certain level of gene expression for a specific gene, and "5" represents a higher level. The sequence depicts how the gene's activity changes over time or in response to a stimulus. Four consecutive periods of low/moderate expression ("2s") are followed by a surge in activity ("5"). This is a highly simplified representation, but it illustrates a possible link.
Practical Applications and Examples
While the interpretations might seem abstract, "2s 2 s 2 2s 5" (or similar sequences) can have concrete applications in various fields:
-
Data Analysis: In data science, such a sequence could represent a pattern in a time series data. For example, analyzing website traffic, four periods of low activity ("2s") followed by a peak ("5"). Identifying and understanding these patterns is crucial for making informed decisions.
-
Security and Cryptography: Simple sequences can be part of more complex encryption algorithms. The "2s" and "5" might represent specific steps in the encryption process, or keys used to transform data.
-
Automation and Robotics: The sequence can be a series of commands for a robot to execute. Each element maps to a specific action or movement. Four steps in a particular direction, followed by a different action based on the "5" command.
-
User Interface (UI) Design: In UI programming, sequences of numbers and letters can represent user interaction patterns. Four clicks on a particular button type, followed by a selection of a different option. Understanding these patterns can inform design decisions and improve user experience.
The Importance of Context
The most crucial takeaway is that the meaning of "2s 2 s 2 2s 5" is entirely dependent on the context in which it's used. Without knowing the specific domain, programming language, musical notation system, or biological system, it's impossible to determine its definitive meaning. The 's' is a particularly important element that drastically changes the interpretation, signaling a modification, type, or shortened duration.
FAQ: Frequently Asked Questions
-
Is "2s 2 s 2 2s 5" a standard code or notation? No, it's not a universally recognized standard. Its meaning is always context-dependent.
-
Can "2s 2 s 2 2s 5" be interpreted as a binary code? Not directly, but you could arbitrarily assign binary values to "2s" and "5" (e.g., "2s" = 01, "5" = 101) and then create a binary sequence.
-
What is the most likely meaning of "2s 2 s 2 2s 5"? Without context, it's impossible to say. In programming, it could be related to array indexing; in music, rhythmic patterns; in math, elements in a sequence.
-
How can I determine the meaning of this sequence in a specific situation? You need to analyze the surrounding information, the field in which it's used, and any available documentation or specifications.
Conclusion: Embracing Ambiguity and the Power of Interpretation
The sequence "2s 2 s 2 2s 5" is a fascinating example of how seemingly simple arrangements of characters can hold diverse meanings depending on the context. From representing array manipulation in computer science to defining rhythmic patterns in music, this sequence showcases the power of interpretation and the importance of understanding the underlying system. While its ambiguity might seem frustrating, it also highlights the flexibility and adaptability of symbolic representation across different disciplines. The real value lies not in finding a single, "correct" answer, but in exploring the various possibilities and appreciating the richness of meaning that can be encoded within a simple sequence. Understanding sequences like this, even seemingly nonsensical ones, encourages critical thinking, problem-solving, and a deeper appreciation for the diverse ways in which information can be represented and communicated.
Latest Posts
Latest Posts
-
Osmosis From One Fluid Compartment To Another Is Determined By
Nov 18, 2025
-
Circle The Correct Choice Within The Parenthesis For 1 18
Nov 18, 2025
-
Jack Is Considering Selling His Elliptical Machine
Nov 18, 2025
-
The Transaction History At An Electronic Goods Store
Nov 18, 2025
-
Which Of The Following Is A Component Of Good Teaching
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 2s 2 S 2 2s 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.