2x X 1 2x 1 X
arrobajuarez
Oct 27, 2025 · 8 min read
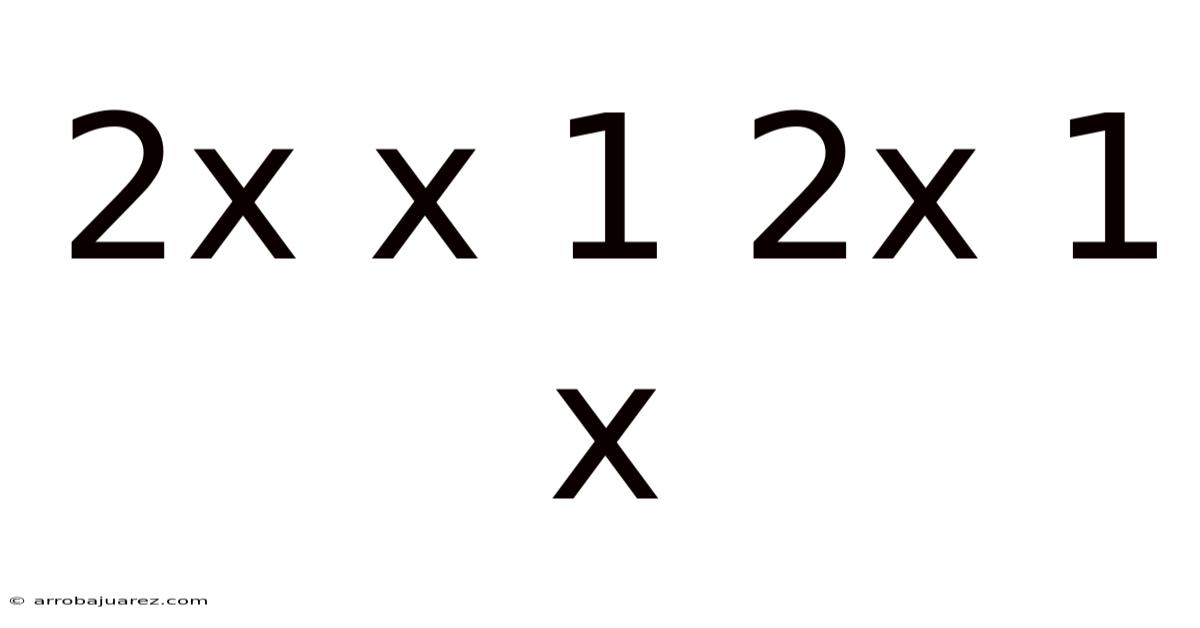
Table of Contents
Here's an in-depth exploration of the mathematical expression "2x × 1 ÷ 2x + 1 × x," examining its potential interpretations, simplification, and behavior within different contexts.
Unpacking the Expression: 2x × 1 ÷ 2x + 1 × x
The expression "2x × 1 ÷ 2x + 1 × x" appears deceptively simple, yet its ambiguity stems from the order of operations. Without explicit parentheses, different interpretations can lead to drastically different results. Let's dissect the possibilities and explore the nuances involved.
The Core Challenge: Order of Operations
In mathematics, the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), dictates the sequence in which operations should be performed. Multiplication and division hold equal precedence and are executed from left to right. Similarly, addition and subtraction share equal precedence and are also performed from left to right.
The ambiguity arises because the expression lacks parentheses to explicitly define the grouping of terms. This opens the door to multiple interpretations, each leading to a unique simplified form.
Possible Interpretations and Simplifications
Let's examine the most common interpretations based on different placements of implicit parentheses:
Interpretation 1: Left-to-Right (Following Strict PEMDAS)
In this interpretation, we strictly adhere to PEMDAS, performing multiplication and division from left to right before moving on to addition.
- 2x × 1 = 2x
- 2x ÷ 2x = 1
- 1 + 1 = 2
- 2 × x = 2x
Therefore, the expression simplifies to 2x.
Interpretation 2: Grouping Multiplication and Division
Here, we might assume an implicit grouping of the multiplication and division operations:
(2x × 1 ÷ 2x) + (1 × x)
- 2x × 1 = 2x
- 2x ÷ 2x = 1
- 1 × x = x
- 1 + x = x + 1
This interpretation leads to the simplified expression x + 1.
Interpretation 3: Grouping Terms with Denominators
This interpretation treats "2x" as a denominator:
(2x × 1) ÷ (2x) + (1 × x)
Which is the same as Interpretation 2 and simplifies to x + 1.
Interpretation 4: Considering the Entire Expression as a Fraction (Unlikely but Possible)
One could argue that the entire expression represents a fraction, although this is less likely given the standard notation:
(2x × 1) / (2x + 1) × x
- 2x × 1 = 2x
- (2x) / (2x + 1) (This fraction remains as is)
- [(2x) / (2x + 1)] × x = (2x²) / (2x + 1)
In this case, the simplified expression is (2x²) / (2x + 1).
A Tabular Summary of Interpretations and Results
| Interpretation | Implicit Parentheses | Simplified Expression |
|---|---|---|
| 1: Strict Left-to-Right PEMDAS | None (applied strictly) | 2x |
| 2: Grouping Multiplication and Division | (2x × 1 ÷ 2x) + (1 × x) | x + 1 |
| 3: Denominator Grouping | (2x × 1) ÷ (2x) + (1 × x) | x + 1 |
| 4: Entire Expression as a Fraction (Unlikely) | (2x × 1) / (2x + 1) × x | (2x²) / (2x + 1) |
The Importance of Clarity: Using Parentheses
The different interpretations highlight the crucial role of parentheses in mathematical expressions. To avoid ambiguity, it's always best practice to explicitly define the order of operations using parentheses. For instance:
- (2x × 1) ÷ (2x + 1) × x clearly represents the fourth interpretation, resulting in (2x²) / (2x + 1).
- (2x × 1 ÷ 2x) + (1 × x) clearly represents the second and third interpretations, resulting in x + 1.
Without parentheses, the expression's meaning remains open to interpretation, potentially leading to errors.
Exploring the Simplified Expressions: A Deeper Dive
Now that we've identified the potential simplified forms, let's analyze each one individually:
1. 2x:
- Linear Function: This represents a simple linear function. The graph is a straight line passing through the origin (0, 0) with a slope of 2.
- Behavior: As x increases, 2x increases proportionally. If x is negative, 2x is also negative.
- Applications: This form is common in scaling problems. For example, if x represents the cost of one item, 2x represents the cost of two identical items.
2. x + 1:
- Linear Function (Shifted): This is also a linear function, but it's shifted vertically. The graph is a straight line with a slope of 1, intersecting the y-axis at the point (0, 1).
- Behavior: As x increases, x + 1 increases linearly. The "+ 1" term ensures that even when x is zero, the expression has a value of 1.
- Applications: This form appears in situations where there's a fixed cost or offset. For example, if x is the number of hours worked and there's a fixed setup fee of $1, then x + 1 represents the total cost.
3. (2x²) / (2x + 1):
- Rational Function: This is a rational function, meaning it's a ratio of two polynomials (2x² and 2x + 1).
- Behavior: The behavior of this function is more complex. It has a vertical asymptote at x = -1/2 (where the denominator is zero). As x approaches infinity, the function also approaches infinity.
- Graph: The graph is a curve with a vertical asymptote. It's not a straight line.
- Applications: This form arises in situations where there's a non-linear relationship between variables, and the rate of change depends on the current value of x. It might model situations in physics or engineering.
Graphical Representation
To visually compare the behavior of these functions, let's consider a graph where we plot all three simplified expressions over a range of x values (e.g., from -5 to 5). (Unfortunately, I can't generate actual graphs here, but I can describe what you'd see).
- 2x: A straight line passing through the origin with a positive slope.
- x + 1: A straight line with a slightly shallower slope than 2x, shifted upwards so it intersects the y-axis at 1.
- (2x²) / (2x + 1): A curve with a vertical asymptote at x = -0.5. The curve approaches this asymptote but never crosses it. For large positive values of x, the curve increases rapidly. For large negative values of x, the curve approaches negative infinity from above the asymptote.
The graph would visually demonstrate how significantly different the functions are, even though they all originated from the same initial expression.
Context Matters: Where Might This Expression Appear?
While the expression "2x × 1 ÷ 2x + 1 × x" itself might not appear directly in many real-world applications, its underlying mathematical principles are fundamental. Let's consider some scenarios where similar structures might arise:
- Algebraic Modeling: When building mathematical models to represent real-world phenomena, expressions like this might appear as intermediate steps in the simplification process. For example, if you're modeling the growth of a population with certain resource constraints, you might encounter a similar expression while solving the governing equations.
- Calculus: In calculus, you might encounter this type of expression when working with derivatives or integrals. Simplification is a key step in solving many calculus problems.
- Computer Programming: When writing code, you might use expressions like this within algorithms. The order of operations is critical to ensure the code produces the correct results. Using parentheses in your code is always a good practice for clarity.
- Engineering: Many engineering problems involve complex equations. Simplifying these equations often leads to expressions with similar mathematical structures.
Examples in Different Fields:
- Physics: Imagine calculating the kinetic energy of an object (1/2 * mv^2). If m and v are themselves defined by more complex expressions, you might end up with something that, after simplification, resembles our initial expression.
- Economics: In supply and demand models, you might have equations that, when combined and simplified, lead to an expression with similar characteristics.
- Finance: Calculating compound interest or present value often involves complex formulas. Simplifying these formulas can produce expressions with related structures.
Common Mistakes and How to Avoid Them
When working with expressions like "2x × 1 ÷ 2x + 1 × x," several common mistakes can lead to incorrect results:
- Ignoring the Order of Operations: Failing to follow PEMDAS correctly is the most frequent error. Always remember to perform multiplication and division from left to right before addition and subtraction.
- Incorrectly Cancelling Terms: Be careful when canceling terms in fractions. You can only cancel factors that are multiplied, not terms that are added or subtracted.
- Assuming Implicit Parentheses: As we've seen, assuming the wrong placement of parentheses can drastically alter the outcome. If in doubt, add parentheses to clarify the intended meaning.
- Algebraic Errors: Careless mistakes in algebraic manipulation (e.g., combining like terms incorrectly) can also lead to errors.
- Not Checking Your Work: It's always a good idea to double-check your work, especially when dealing with complex expressions. If possible, substitute numerical values for x to verify that your simplified expression produces the same result as the original.
Best Practices for Accuracy:
- Always Use Parentheses: When in doubt, add parentheses to explicitly define the order of operations.
- Work Step-by-Step: Break down the problem into smaller, manageable steps.
- Double-Check Each Step: Verify that each step is correct before moving on to the next.
- Simplify Carefully: Pay close attention to algebraic manipulations.
- Check Your Answer: Substitute numerical values to verify your solution.
Conclusion: The Power of Precision
The seemingly simple expression "2x × 1 ÷ 2x + 1 × x" serves as a powerful illustration of the importance of precision and clarity in mathematics. Its ambiguity highlights the critical role of the order of operations and the necessity of using parentheses to avoid misinterpretations.
By carefully considering the different possible interpretations and simplifying them step-by-step, we arrive at multiple distinct results. Each simplified expression represents a different mathematical function with its own unique behavior and potential applications.
The key takeaway is that mathematical expressions are not just strings of symbols; they are precise statements with specific meanings. Understanding the rules of mathematics and applying them diligently is essential for arriving at correct and meaningful conclusions. Therefore, always strive for clarity, use parentheses liberally, and double-check your work to avoid the pitfalls of ambiguity.
Latest Posts
Latest Posts
-
No Spell Out The Full Name Of The Compound
Oct 27, 2025
-
A Company Uses The Allowance Method To Account
Oct 27, 2025
-
Question Elvis Part C Select The Correct Configuration
Oct 27, 2025
-
Demand Is Said To Be Inelastic When
Oct 27, 2025
-
Question Hamburger You Are Given Either An Aldehyde Or Ketone
Oct 27, 2025
Related Post
Thank you for visiting our website which covers about 2x X 1 2x 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.