3 X 1 5 X 1
arrobajuarez
Oct 27, 2025 · 8 min read
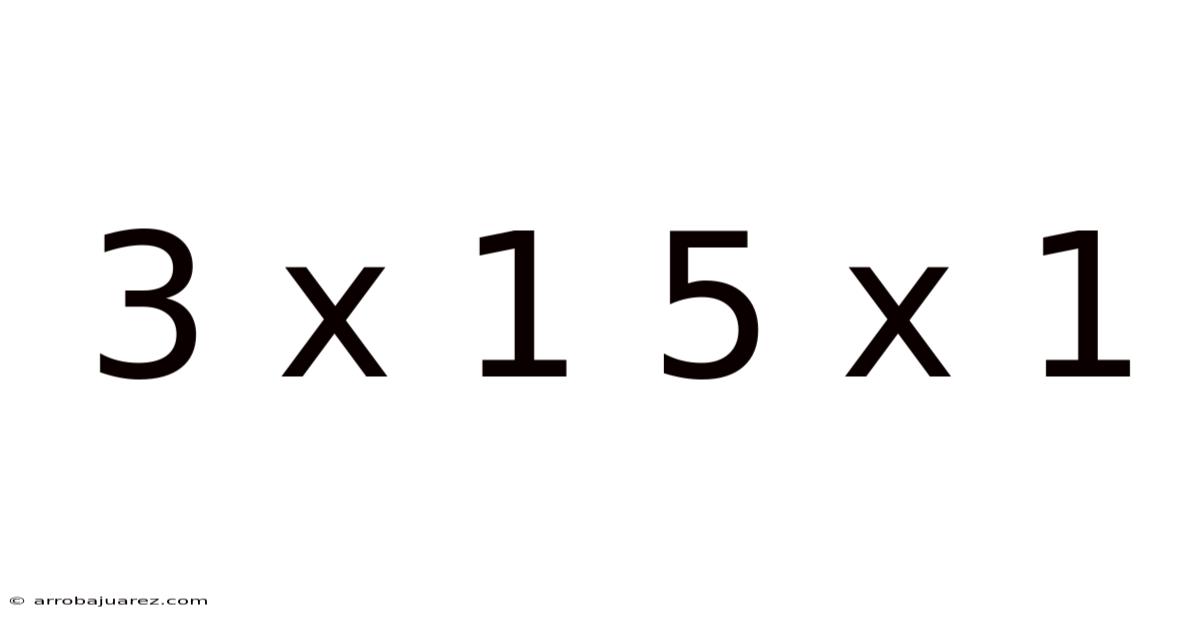
Table of Contents
The realm of mathematics, often perceived as a complex domain, reveals its elegance through seemingly simple operations. Delving into the expressions 3 x 1 and 5 x 1, we uncover fundamental principles of multiplication and identity, which serve as building blocks for more advanced mathematical concepts. This exploration will not only clarify the results of these operations but also illuminate the underlying mathematical truths they represent.
Understanding Multiplication
Multiplication, at its core, is a shorthand for repeated addition. The expression a x b signifies adding the number a to itself b times. For instance, 3 x 4 is equivalent to 3 + 3 + 3 + 3, resulting in 12. This understanding forms the basis for grasping the significance of multiplying by one.
The Identity Property of Multiplication
The identity property of multiplication states that any number multiplied by one equals that number itself. In mathematical notation, this is expressed as a x 1 = a. This property holds true for all real numbers, including integers, fractions, decimals, and irrational numbers. The number one is therefore termed the multiplicative identity, as it preserves the identity of the number it multiplies.
3 x 1: A Detailed Look
Applying the identity property to the expression 3 x 1, we can confidently state that the result is 3. This can be visualized as adding the number 3 to itself one time, which simply yields 3. In the context of real-world applications, this could represent having one group of three objects, resulting in a total of three objects.
5 x 1: A Detailed Look
Similarly, for the expression 5 x 1, the identity property of multiplication dictates that the result is 5. This signifies having one group of five objects, which equates to a total of five objects. The simplicity of this operation belies its fundamental importance in various mathematical and practical scenarios.
Visual Representations and Examples
To further illustrate these concepts, consider the following visual representations:
- 3 x 1: Imagine three apples in a single basket. The total number of apples is three.
- 5 x 1: Picture five coins on a table. The total value, assuming each coin is worth one unit, is five units.
These simple examples underscore the direct and intuitive nature of multiplying by one.
The Significance of the Identity Property
The identity property of multiplication is not merely a mathematical curiosity; it is a cornerstone of numerous mathematical operations and concepts. Its significance is evident in:
- Algebra: Simplifying algebraic expressions often involves multiplying terms by one in various forms (e.g., (x/x) = 1, where x ≠ 0) to manipulate equations without changing their inherent value.
- Fractions: Converting fractions to equivalent forms relies on the identity property. For instance, to convert 1/2 to an equivalent fraction with a denominator of 4, we multiply both the numerator and denominator by 2: (1/2) x (2/2) = 2/4.
- Unit Conversions: Converting units of measurement involves multiplying by conversion factors that are essentially equal to one. For example, converting meters to centimeters involves multiplying by 100 cm/1 m, which is equal to one.
Advanced Applications
While the expressions 3 x 1 and 5 x 1 are elementary, the underlying principle extends to more advanced mathematical domains:
- Matrix Algebra: In matrix algebra, the identity matrix (a square matrix with ones on the main diagonal and zeros elsewhere) acts as the multiplicative identity. Multiplying any matrix by the identity matrix results in the original matrix.
- Complex Numbers: The identity property holds true for complex numbers as well. Multiplying any complex number by one leaves the number unchanged.
- Abstract Algebra: In abstract algebra, the concept of a multiplicative identity is generalized to algebraic structures known as groups and rings. These structures have a designated element that, when combined with any other element using the defined operation, leaves the other element unchanged.
Common Misconceptions
Despite the simplicity of multiplying by one, some common misconceptions can arise:
- Confusion with Addition: Some individuals may confuse multiplication by one with addition by one. It is crucial to emphasize that a x 1 = a, whereas a + 1 results in a different value.
- Zero Property: Another common misconception is confusing the identity property with the zero property of multiplication, which states that any number multiplied by zero equals zero. a x 0 = 0 is distinct from a x 1 = a.
- Overcomplicating the Concept: The simplicity of multiplying by one can sometimes lead to overthinking. It is important to remember that multiplying by one simply preserves the original value.
The Role of Multiplication in Everyday Life
Multiplication, in general, plays a pivotal role in numerous aspects of everyday life:
- Calculating Costs: Determining the total cost of multiple items involves multiplication. For example, if each item costs $3 and you purchase 5 items, the total cost is 3 x 5 = $15.
- Measuring Areas and Volumes: Calculating the area of a rectangle (length x width) or the volume of a cube (side x side x side) relies on multiplication.
- Scaling Recipes: Adjusting recipe quantities for a different number of servings involves multiplying the original ingredient amounts by a scaling factor.
- Financial Calculations: Computing interest, calculating loan payments, and determining investment returns all involve multiplication.
Exploring Further: Beyond Basic Multiplication
Understanding 3 x 1 and 5 x 1 provides a foundation for exploring more complex multiplication scenarios:
- Multiplication Tables: Memorizing multiplication tables (e.g., the 3 times table, the 5 times table) builds fluency and speed in performing multiplication operations.
- Long Multiplication: Long multiplication is a method for multiplying larger numbers by breaking down the operation into smaller, more manageable steps.
- Scientific Notation: Scientific notation uses powers of ten to express very large or very small numbers in a compact form. Multiplication is used to manipulate numbers expressed in scientific notation.
Practical Exercises
To reinforce understanding, consider the following practical exercises:
- Visual Representation: Draw visual representations for the following expressions:
- 7 x 1
- 10 x 1
- 1 x 1
- Real-World Problems: Create real-world scenarios that involve multiplying by one. For example:
- A box contains 8 pencils. How many pencils are in one box?
- A recipe calls for 2 cups of flour. If you make one batch of the recipe, how much flour do you need?
- Algebraic Simplification: Simplify the following algebraic expressions:
- 5x * 1
- (3y + 2) * 1
- (a/b) * 1, where b ≠ 0
The Importance of Conceptual Understanding
While memorizing multiplication facts and procedures is valuable, developing a deep conceptual understanding of multiplication is crucial for long-term mathematical success. This includes grasping the relationship between multiplication and repeated addition, understanding the identity property, and recognizing the role of multiplication in various mathematical contexts.
The Beauty of Simplicity
The expressions 3 x 1 and 5 x 1, while seemingly simple, encapsulate fundamental mathematical principles that underpin a vast array of mathematical concepts and applications. By understanding the identity property of multiplication, we gain a deeper appreciation for the elegance and interconnectedness of mathematics.
Conclusion
In summary, 3 x 1 equals 3 and 5 x 1 equals 5, due to the identity property of multiplication. This property asserts that any number multiplied by one remains unchanged. This foundational concept is not only crucial for basic arithmetic but also extends to more advanced mathematical fields, including algebra, matrix algebra, and abstract algebra. A solid understanding of this principle enhances mathematical fluency and provides a strong base for tackling more complex mathematical challenges.
Frequently Asked Questions (FAQ)
-
What is the identity property of multiplication?
The identity property of multiplication states that any number multiplied by one equals that number itself (a x 1 = a).
-
Why is the identity property important?
It is important because it forms the basis for many mathematical operations, including simplifying algebraic expressions, converting fractions, and performing unit conversions.
-
Is the identity property true for all numbers?
Yes, the identity property holds true for all real numbers, including integers, fractions, decimals, and irrational numbers, as well as complex numbers.
-
How does the identity property relate to everyday life?
It relates to everyday life through calculations involving costs, measurements, recipes, and financial transactions, where multiplication is commonly used.
-
What is the difference between the identity property and the zero property of multiplication?
The identity property states that any number multiplied by one equals that number, while the zero property states that any number multiplied by zero equals zero. They are distinct properties with different outcomes.
-
Can the identity property be applied in algebra?
Yes, the identity property is frequently used in algebra to simplify expressions and manipulate equations without changing their values.
-
Are there any common mistakes people make when multiplying by one?
Common mistakes include confusing multiplication by one with addition by one, confusing the identity property with the zero property, and overcomplicating the concept.
-
How can I improve my understanding of multiplication?
You can improve your understanding by memorizing multiplication tables, practicing long multiplication, and focusing on the conceptual understanding of multiplication as repeated addition.
-
Does the identity property apply to matrices?
Yes, in matrix algebra, the identity matrix acts as the multiplicative identity. Multiplying any matrix by the identity matrix results in the original matrix.
-
Where else can I use multiplication in my daily life?
You can use multiplication in various daily activities such as calculating distances, estimating travel times, determining quantities for cooking, and managing personal finances.
Latest Posts
Latest Posts
-
What Is The Length Of The Arc Shown In Red
Oct 27, 2025
-
Math 1314 Lab Module 1 Answers
Oct 27, 2025
-
Which Of The Following Best Describes Temperature
Oct 27, 2025
-
Arrange The Values According To Absolute Value
Oct 27, 2025
-
Classical And Operant Conditioning Are Forms Of Learning
Oct 27, 2025
Related Post
Thank you for visiting our website which covers about 3 X 1 5 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.