Draw The Vector C⃗ 0.5 A⃗ 2b⃗
arrobajuarez
Dec 06, 2025 · 9 min read
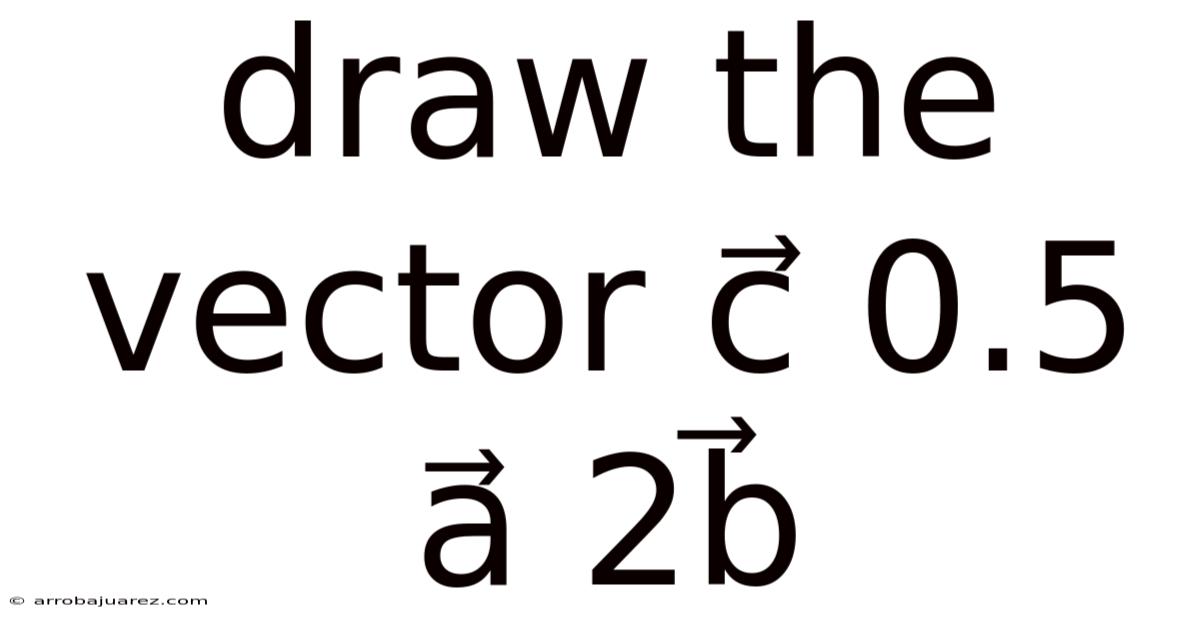
Table of Contents
Let's explore how to visualize and draw the vector c = 0.5a + 2b. This seemingly simple vector equation opens the door to understanding vector operations, scalar multiplication, and vector addition, all fundamental concepts in linear algebra and physics. Whether you're a student learning the basics or a professional needing a refresher, this guide will break down the process step-by-step, making it easy to grasp and apply.
Understanding the Building Blocks: Vectors a and b
Before we can construct the vector c, we need to understand what a and b represent. Vectors are mathematical objects that have both magnitude (length) and direction. They're often represented graphically as arrows. The length of the arrow corresponds to the magnitude of the vector, and the direction of the arrow indicates the vector's direction.
For this exercise, let's assume we have the following vectors defined in a 2-dimensional Cartesian coordinate system (x, y):
- a = (2, 1)
- b = (-1, 3)
These vectors can be visually represented on a graph. The vector a starts at the origin (0, 0) and extends to the point (2, 1). Similarly, b starts at (0, 0) and ends at (-1, 3). Keep this visual in mind as we proceed.
Scalar Multiplication: Resizing Vectors
The equation c = 0.5a + 2b involves scalar multiplication. Scalar multiplication means multiplying a vector by a scalar (a number). This operation changes the magnitude (length) of the vector but doesn't change its direction (unless the scalar is negative, in which case it reverses the direction).
-
0.5a: This means we're multiplying the vector a by the scalar 0.5. To perform scalar multiplication, we multiply each component of the vector by the scalar.
- 5a = 0.5 * (2, 1) = (0.5 * 2, 0.5 * 1) = (1, 0.5)
The vector 0.5a is now shorter than the original vector a, having half its length. It still points in the same direction.
-
2b: This means we're multiplying the vector b by the scalar 2. Again, we multiply each component of the vector by the scalar.
- b = 2 * (-1, 3) = (2 * -1, 2 * 3) = (-2, 6)
The vector 2b is now twice as long as the original vector b, pointing in the same direction.
Vector Addition: Combining Vectors
Now that we've performed the scalar multiplications, we're left with the task of vector addition. Vector addition combines two or more vectors to produce a resultant vector. There are two primary ways to visualize vector addition: the head-to-tail method and the parallelogram method. We'll focus on the head-to-tail method as it's more intuitive for this explanation.
Head-to-Tail Method
-
Start with the first vector: Begin with the vector 0.5a = (1, 0.5). Draw this vector on your coordinate system, starting at the origin (0, 0) and ending at (1, 0.5).
-
Place the second vector's tail at the first vector's head: Instead of drawing the vector 2b = (-2, 6) starting at the origin, start it at the head of the vector 0.5a, which is the point (1, 0.5). Draw the vector 2b from (1, 0.5). This means you will end up at the point (1 + (-2), 0.5 + 6) = (-1, 6.5).
-
Draw the resultant vector: The resultant vector c is the vector that starts at the origin (0, 0) and ends at the head of the last vector you drew (in this case, the head of 2b which is the point (-1, 6.5)).
Mathematical Calculation
We can also calculate the vector c mathematically by adding the components of the vectors 0.5a and 2b:
c = 0.5a + 2b = (1, 0.5) + (-2, 6) = (1 + (-2), 0.5 + 6) = (-1, 6.5)
Therefore, c = (-1, 6.5). This confirms the result we obtained graphically using the head-to-tail method.
Drawing the Vector c = (-1, 6.5)
Now that we know the components of vector c, we can draw it on our coordinate system.
-
Start at the origin: Begin at the point (0, 0).
-
Extend to the endpoint: Draw an arrow from the origin (0, 0) to the point (-1, 6.5). This arrow represents the vector c.
Software and Tools for Visualization
While drawing vectors by hand is helpful for understanding the concepts, various software and online tools can make the process easier and more precise. Here are a few options:
- GeoGebra: A free and powerful software for geometry, algebra, calculus, and more. It allows you to define vectors, perform operations, and visualize the results in real-time.
- MATLAB: A popular software for numerical computation, visualization, and programming. It has excellent tools for working with vectors and matrices.
- Python with NumPy and Matplotlib: Python is a versatile programming language with libraries like NumPy (for numerical operations) and Matplotlib (for plotting). This combination is excellent for creating custom vector visualizations.
- Online Vector Calculators: Several websites offer vector calculators and visualizers. Simply input the vector components and the calculator will draw the vector for you.
A Deeper Dive: Vector Spaces and Linear Combinations
The operation c = 0.5a + 2b is an example of a linear combination of vectors. In general, a linear combination of vectors v1, v2, ..., vn is an expression of the form:
c1v1 + c2v2 + ... + cnvn
where c1, c2, ..., cn are scalars. The set of all possible linear combinations of a set of vectors forms a vector space.
Vector Space
A vector space is a mathematical structure that allows for vector addition and scalar multiplication. The most common example is the 2-dimensional Cartesian plane (R²) or the 3-dimensional space (R³), but vector spaces can be more abstract.
Linear Independence
Two vectors are linearly independent if neither can be written as a scalar multiple of the other. In our example, a and b are linearly independent because there is no scalar k such that a = k*b. If vectors are linearly independent, they can "span" a vector space, meaning any vector in that space can be written as a linear combination of those vectors.
Applications in Physics and Engineering
Vectors are fundamental to many areas of physics and engineering. Here are just a few examples:
- Forces: Forces are vector quantities. The net force on an object is the vector sum of all the individual forces acting on it.
- Velocities and Accelerations: Velocity and acceleration are also vector quantities. Understanding how to add and subtract velocities is crucial in analyzing motion.
- Fields: Electric and magnetic fields are vector fields, meaning that at each point in space, there is a vector associated with the field.
- Computer Graphics: Vectors are used extensively in computer graphics to represent positions, directions, and normals of surfaces.
Common Mistakes to Avoid
- Incorrect Scalar Multiplication: Make sure to multiply each component of the vector by the scalar. It's a common mistake to only multiply one component.
- Misunderstanding Vector Addition: Remember to use either the head-to-tail method or the parallelogram method correctly. Simply adding the magnitudes of the vectors is incorrect.
- Ignoring Direction: Vectors have direction! Don't treat them as just numbers. Always consider the direction when performing vector operations.
- Confusing Vectors and Scalars: Vectors have both magnitude and direction, while scalars only have magnitude. Don't mix them up in your calculations.
Expanding the Concept: 3D Vectors
The concepts we've discussed easily extend to 3-dimensional vectors. A 3D vector is represented by three components (x, y, z). Scalar multiplication and vector addition are performed in the same way, but now you have three components to consider. Visualizing 3D vectors can be more challenging, but software tools like GeoGebra can be helpful.
For example, let's say we have the following 3D vectors:
- a = (1, 2, 3)
- b = (-1, 0, 2)
Then, to find c = 0.5a + 2b, we would perform the following calculations:
- 5a = 0.5 * (1, 2, 3) = (0.5, 1, 1.5)
- b = 2 * (-1, 0, 2) = (-2, 0, 4) c = 0.5a + 2b = (0.5, 1, 1.5) + (-2, 0, 4) = (-1.5, 1, 5.5)
Therefore, c = (-1.5, 1, 5.5).
Key Takeaways and Further Exploration
Understanding vector operations is essential for anyone studying mathematics, physics, engineering, or computer science. Being able to visualize and manipulate vectors allows you to solve a wide range of problems.
- Vectors have magnitude and direction.
- Scalar multiplication changes the magnitude of a vector.
- Vector addition combines vectors to produce a resultant vector.
- Linear combinations are fundamental in linear algebra.
- Vectors have numerous applications in physics, engineering, and computer graphics.
To further your understanding, consider exploring these topics:
- Dot product and cross product: These are two important operations that can be performed on vectors.
- Matrices: Matrices are arrays of numbers that can be used to represent linear transformations of vectors.
- Linear transformations: These are functions that map vectors to other vectors in a linear way.
- Eigenvalues and eigenvectors: These are special vectors that are unchanged (except for a scalar multiple) when a linear transformation is applied.
FAQs: Addressing Common Questions
-
What is the difference between a vector and a scalar? A vector has both magnitude and direction, while a scalar only has magnitude. Examples of scalars include temperature, mass, and speed. Examples of vectors include velocity, force, and displacement.
-
How do I find the magnitude of a vector? The magnitude of a vector v = (x, y) is given by ||v|| = √(x² + y²). In 3D, the magnitude of a vector v = (x, y, z) is given by ||v|| = √(x² + y² + z²).
-
What is a unit vector? A unit vector is a vector with a magnitude of 1. Any vector can be normalized to create a unit vector by dividing the vector by its magnitude.
-
Why are vectors important? Vectors are used to represent quantities that have both magnitude and direction. They are fundamental to many areas of science and engineering, including physics, computer graphics, and data analysis.
-
How do I add vectors graphically? Use the head-to-tail method or the parallelogram method. In the head-to-tail method, place the tail of the second vector at the head of the first vector. The resultant vector is the vector that starts at the origin and ends at the head of the last vector.
By mastering these fundamental concepts and practicing with examples, you'll be well-equipped to tackle more advanced topics in linear algebra and its applications. Understanding how to draw and manipulate vectors is a valuable skill that will serve you well in many fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Draw The Vector C⃗ 0.5 A⃗ 2b⃗ . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.