Evaluate The Definite Integral 1 3 1 7x Dx 0
arrobajuarez
Oct 30, 2025 · 7 min read
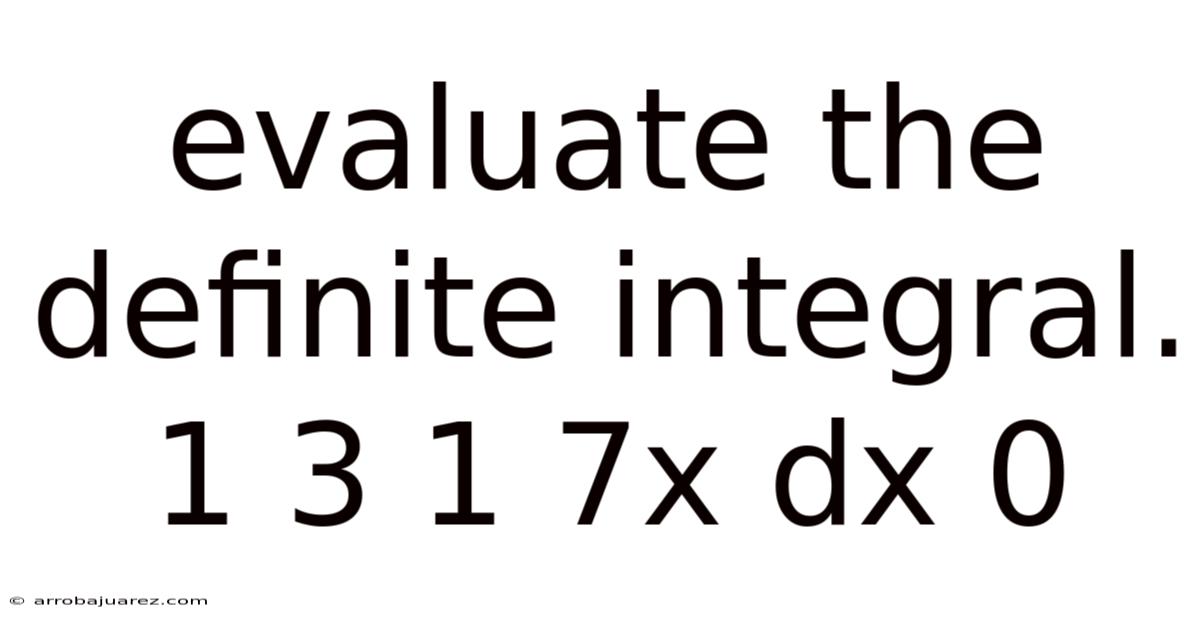
Table of Contents
Evaluating definite integrals might seem daunting at first, but with a systematic approach and a solid understanding of calculus fundamentals, it becomes a manageable task. This article delves into the process of evaluating the definite integral ∫[0 to 1] (1 / (7x + 1)^(1/3)) dx, providing a step-by-step guide, explaining the underlying concepts, and offering insights into the solution.
Understanding Definite Integrals
A definite integral represents the area under a curve between two specified limits. In the given problem, we're tasked with finding the area under the curve of the function f(x) = 1 / (7x + 1)^(1/3) between the limits x = 0 and x = 1. This area can be calculated using the fundamental theorem of calculus.
Step-by-Step Solution: Evaluating the Definite Integral
Let's break down the process of evaluating the definite integral ∫[0 to 1] (1 / (7x + 1)^(1/3)) dx:
1. Indefinite Integration:
The first step is to find the indefinite integral of the function f(x) = 1 / (7x + 1)^(1/3). This means finding a function F(x) such that its derivative F'(x) equals f(x). We can achieve this using a substitution method.
2. Substitution:
Let u = 7x + 1. This implies that du/dx = 7, or dx = (1/7) du. Now we can rewrite the integral in terms of 'u':
∫ (1 / (7x + 1)^(1/3)) dx = ∫ (1 / u^(1/3)) * (1/7) du = (1/7) ∫ u^(-1/3) du
3. Power Rule for Integration:
Apply the power rule for integration, which states that ∫x^n dx = (x^(n+1)) / (n+1) + C, where C is the constant of integration.
(1/7) ∫ u^(-1/3) du = (1/7) * (u^(2/3) / (2/3)) + C = (3/14) * u^(2/3) + C
4. Substitute Back:
Replace 'u' with its original expression in terms of 'x':
(3/14) * u^(2/3) + C = (3/14) * (7x + 1)^(2/3) + C
Therefore, the indefinite integral of f(x) is F(x) = (3/14) * (7x + 1)^(2/3) + C.
5. Applying the Fundamental Theorem of Calculus:
The fundamental theorem of calculus states that the definite integral of a function f(x) from a to b is equal to F(b) - F(a), where F(x) is the indefinite integral of f(x).
In our case, a = 0 and b = 1. So, we need to calculate F(1) and F(0).
6. Evaluating F(1):
F(1) = (3/14) * (7(1) + 1)^(2/3) = (3/14) * (8)^(2/3) = (3/14) * (2^3)^(2/3) = (3/14) * 2^2 = (3/14) * 4 = 6/7
7. Evaluating F(0):
F(0) = (3/14) * (7(0) + 1)^(2/3) = (3/14) * (1)^(2/3) = (3/14) * 1 = 3/14
8. Calculating the Definite Integral:
Finally, subtract F(0) from F(1):
∫[0 to 1] (1 / (7x + 1)^(1/3)) dx = F(1) - F(0) = (6/7) - (3/14) = (12/14) - (3/14) = 9/14
Therefore, the value of the definite integral ∫[0 to 1] (1 / (7x + 1)^(1/3)) dx is 9/14.
Deeper Dive: Understanding the Concepts
To fully grasp the solution, let's delve into the underlying concepts:
- Integration: Integration is the reverse process of differentiation. It allows us to find the area under a curve, accumulated change, and other important quantities.
- Indefinite Integral: The indefinite integral represents the family of functions whose derivative is equal to the given function. It includes a constant of integration, "C," because the derivative of a constant is always zero.
- Definite Integral: The definite integral calculates the precise area under a curve between two specific limits. It does not include the constant of integration because it cancels out when evaluating F(b) - F(a).
- Substitution Method (u-substitution): This technique simplifies complex integrals by replacing a part of the integrand with a new variable, 'u'. The goal is to transform the integral into a simpler form that can be easily integrated using standard rules.
- Power Rule for Integration: A fundamental rule that states ∫x^n dx = (x^(n+1)) / (n+1) + C, valid for all n ≠ -1.
- Fundamental Theorem of Calculus: This theorem connects differentiation and integration. It states that the definite integral of a function f(x) from a to b is equal to F(b) - F(a), where F(x) is any antiderivative of f(x).
Common Mistakes to Avoid
Evaluating definite integrals can be tricky. Here are some common mistakes to watch out for:
- Forgetting the Constant of Integration (C) for Indefinite Integrals: While it doesn't affect the definite integral calculation, it's crucial to include it when finding the indefinite integral.
- Incorrectly Applying the Power Rule: Double-check that you're adding 1 to the exponent and dividing by the new exponent correctly.
- Failing to Substitute Back: After using u-substitution, remember to replace 'u' with its original expression in terms of 'x' before evaluating the definite integral.
- Incorrectly Changing Limits of Integration: If you change the variable of integration (e.g., using u-substitution), you must also change the limits of integration to correspond to the new variable. In this example, we didn't need to change the limits because we substituted back to x before evaluating. However, we could have changed them: When x = 0, u = 7(0) + 1 = 1. When x = 1, u = 7(1) + 1 = 8. So, the integral could also be written as ∫[1 to 8] (1/7) * u^(-1/3) du, which would lead to the same answer.
- Arithmetic Errors: Simple calculation mistakes can lead to incorrect results. Carefully double-check your arithmetic.
Applications of Definite Integrals
Definite integrals have numerous applications in various fields:
- Physics: Calculating displacement, work done by a force, and center of mass.
- Engineering: Determining areas, volumes, and moments of inertia.
- Economics: Calculating consumer surplus and producer surplus.
- Probability: Finding probabilities associated with continuous random variables.
- Statistics: Calculating expected values and variances.
Practice Problems
To solidify your understanding, try evaluating these definite integrals:
- ∫[0 to 2] x^2 dx
- ∫[1 to 3] (2x + 1) dx
- ∫[0 to π/2] sin(x) dx
- ∫[0 to 1] e^x dx
Advanced Techniques for Evaluating Integrals
While the substitution method and power rule are powerful tools, more complex integrals may require advanced techniques:
- Integration by Parts: Used to integrate products of functions. The formula is ∫u dv = uv - ∫v du.
- Trigonometric Substitution: Used for integrals involving square roots of quadratic expressions.
- Partial Fraction Decomposition: Used to integrate rational functions (ratios of polynomials).
- Improper Integrals: Integrals where one or both limits of integration are infinite or the integrand has a discontinuity within the interval of integration. These require special handling involving limits.
- Numerical Integration: When an integral cannot be evaluated analytically (i.e., using symbolic methods), numerical methods like the trapezoidal rule or Simpson's rule can be used to approximate the value of the integral.
The Importance of Practice
Mastering the evaluation of definite integrals requires consistent practice. Work through numerous examples, gradually increasing the complexity of the problems. The more you practice, the more comfortable you'll become with identifying the appropriate integration techniques and avoiding common mistakes.
Tips for Success
- Review Calculus Fundamentals: Ensure you have a solid understanding of differentiation, integration, and trigonometric functions.
- Master Basic Integration Rules: Memorize and practice using the power rule, trigonometric integral rules, and exponential integral rules.
- Learn Substitution Techniques: Practice u-substitution and trigonometric substitution to simplify complex integrals.
- Understand the Fundamental Theorem of Calculus: This is the cornerstone of evaluating definite integrals.
- Check Your Work: Always double-check your calculations to avoid arithmetic errors. You can also use online integral calculators to verify your results.
- Seek Help When Needed: Don't hesitate to ask for help from your instructor, classmates, or online resources if you're struggling with a particular problem.
Conclusion
Evaluating the definite integral ∫[0 to 1] (1 / (7x + 1)^(1/3)) dx involves a systematic application of integration techniques and the fundamental theorem of calculus. By understanding the underlying concepts, mastering the substitution method, and avoiding common mistakes, you can confidently tackle similar problems. Remember that practice is key to success in calculus. The more you practice, the more comfortable you'll become with the process, and the better you'll understand the power and versatility of definite integrals in various applications. Keep practicing, and you'll be well on your way to mastering integral calculus! This example highlights how breaking down a complex problem into smaller, manageable steps, combined with a solid understanding of the underlying theory, can lead to a successful solution. Good luck!
Latest Posts
Related Post
Thank you for visiting our website which covers about Evaluate The Definite Integral 1 3 1 7x Dx 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.