Evaluate The Definite Integral. 2 E 1/x4 X5 Dx 1
arrobajuarez
Oct 27, 2025 · 8 min read
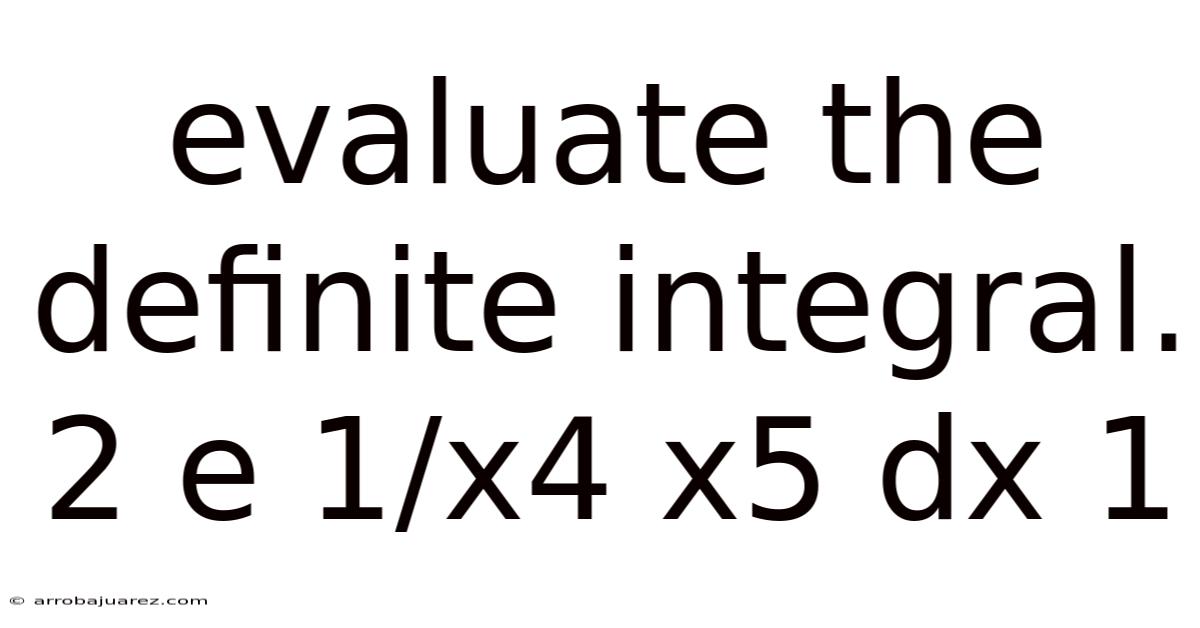
Table of Contents
Evaluating definite integrals can seem daunting at first, but understanding the fundamental concepts and applying the right techniques can simplify the process significantly. This article delves into a comprehensive exploration of how to evaluate the definite integral ∫[1 to 2] e^(1/x^4) / x^5 dx, providing step-by-step solutions, explanations, and insights to enhance your understanding. We will cover the necessary calculus principles, integration strategies, and common pitfalls to avoid, ensuring you are well-equipped to tackle similar problems.
Introduction to Definite Integrals
A definite integral is a fundamental concept in calculus that represents the area under a curve between two specified limits. Mathematically, it is written as ∫[a to b] f(x) dx, where a and b are the lower and upper limits of integration, respectively, and f(x) is the integrand. Evaluating a definite integral involves finding the antiderivative of f(x) and then computing the difference between the antiderivative evaluated at the upper and lower limits.
The given definite integral is ∫[1 to 2] e^(1/x^4) / x^5 dx. To solve this, we will employ a substitution method, carefully changing the variable to simplify the integral into a more manageable form.
Step-by-Step Solution
1. Identify the Appropriate Substitution
The key to solving this integral lies in recognizing a suitable substitution. Notice that the derivative of 1/x^4 is related to x^-5, which appears in the integral. This suggests that we should let u = 1/x^4.
Therefore, we set: u = 1/x^4
2. Compute the Derivative of u with Respect to x
Next, we need to find du/dx. Differentiating u with respect to x gives: du/dx = -4/x^5
We can rearrange this to express dx in terms of du: dx = -x^5/4 du
3. Substitute u and dx into the Original Integral
Now we substitute u and dx into the original integral ∫[1 to 2] e^(1/x^4) / x^5 dx:
∫ e^u / x^5 (-x^5/4) du
The x^5 terms cancel out, leaving us with: ∫ -1/4 e^u du
4. Adjust the Limits of Integration
Since we have changed the variable from x to u, we need to adjust the limits of integration accordingly.
- When x = 1, u = 1/1^4 = 1
- When x = 2, u = 1/2^4 = 1/16
Our new limits of integration are from 1 to 1/16. Thus, the integral becomes: ∫[1 to 1/16] -1/4 e^u du
5. Evaluate the Integral
We can now evaluate the simplified integral: -1/4 ∫[1 to 1/16] e^u du
The antiderivative of e^u is simply e^u. Therefore, we have: -1/4 [e^u] from 1 to 1/16
Which evaluates to: -1/4 (e^(1/16) - e^1)
6. Simplify the Result
Finally, we simplify the result: -1/4 (e^(1/16) - e) 1/4 (e - e^(1/16))
Therefore, the definite integral ∫[1 to 2] e^(1/x^4) / x^5 dx evaluates to 1/4 (e - e^(1/16)).
Common Mistakes and How to Avoid Them
Evaluating definite integrals can be tricky, and there are several common mistakes that students often make. Here’s how to avoid them:
1. Forgetting to Change the Limits of Integration
One of the most common errors is forgetting to change the limits of integration when performing a substitution. Remember that when you change the variable from x to u, the limits must also be transformed to reflect the new variable. Always compute the new limits by substituting the original limits into the substitution equation.
How to avoid: After determining your substitution u = g(x), immediately calculate the new limits:
- Lower limit: u_lower = g(a)
- Upper limit: u_upper = g(b)
2. Incorrectly Computing the Derivative
Another common mistake is incorrectly computing the derivative of the substitution variable. Double-check your derivative calculations to ensure accuracy.
How to avoid: Use derivative rules carefully and verify your work, especially when dealing with complex functions. A small error in the derivative can propagate through the rest of the problem.
3. Not Simplifying the Integral Correctly
Simplification errors can occur when substituting u and du into the original integral. Make sure to properly cancel out terms and simplify the expression before integrating.
How to avoid: Take your time and carefully simplify the integral after each substitution step. Ensure that all x terms are replaced with u terms (or constants).
4. Forgetting the Constant of Integration for Indefinite Integrals
While evaluating definite integrals, we don't need to add a constant of integration (+C), but it's crucial to remember this constant when dealing with indefinite integrals.
How to avoid: Understand the difference between definite and indefinite integrals. Definite integrals have limits and yield a numerical value, whereas indefinite integrals do not have limits and yield a function plus a constant.
5. Algebraic Errors
Simple algebraic errors, such as incorrect signs or exponent manipulations, can lead to incorrect results.
How to avoid: Pay close attention to detail when performing algebraic manipulations. Double-check your work, especially when dealing with negative signs or fractions.
Advanced Integration Techniques
While substitution works for the given integral, other integration techniques are crucial for more complex problems. Here are a few:
1. Integration by Parts
Integration by parts is used when the integrand is a product of two functions. The formula is: ∫ u dv = uv - ∫ v du
Choosing the right u and dv can significantly simplify the integral.
2. Trigonometric Substitution
Trigonometric substitution is useful when the integrand contains expressions of the form √(a^2 - x^2), √(a^2 + x^2), or √(x^2 - a^2). By substituting x with a trigonometric function, you can simplify the integral.
3. Partial Fraction Decomposition
Partial fraction decomposition is used to integrate rational functions (ratios of polynomials). This technique involves breaking down the rational function into simpler fractions that are easier to integrate.
4. Numerical Integration
When analytical methods fail, numerical integration techniques such as the trapezoidal rule, Simpson's rule, and Monte Carlo integration can be used to approximate the value of the definite integral.
Real-World Applications
Definite integrals have numerous applications across various fields:
1. Physics
In physics, definite integrals are used to calculate displacement, velocity, and acceleration of moving objects. They are also used to determine the work done by a force and the center of mass of an object.
2. Engineering
Engineers use definite integrals to calculate areas, volumes, and moments of inertia, which are essential in structural analysis and design. They are also used in fluid dynamics to calculate flow rates and pressures.
3. Economics
In economics, definite integrals are used to calculate consumer surplus, producer surplus, and present value of future income streams.
4. Statistics
Definite integrals are used in probability theory to calculate probabilities associated with continuous random variables.
5. Computer Graphics
In computer graphics, definite integrals are used to calculate areas and volumes of 3D models, which is essential for rendering and shading.
Elaborating on the Substitution Method
The substitution method, also known as u-substitution, is a powerful technique for simplifying integrals. The key idea is to replace a complicated expression within the integral with a single variable, making the integral easier to evaluate. Here’s a more detailed look at the process:
1. Choosing the Right Substitution
The most critical step is identifying a suitable substitution. Look for expressions within the integral whose derivative is also present (up to a constant multiple). Common choices include:
- Expressions inside parentheses or under radicals
- Denominators of fractions
- Arguments of trigonometric, exponential, or logarithmic functions
2. Performing the Substitution
Once you’ve chosen your substitution u = g(x), compute its derivative du/dx = g'(x). Then, solve for dx in terms of du: dx = du / g'(x)
Substitute u and dx into the original integral. The goal is to eliminate all x terms and express the integral solely in terms of u.
3. Adjusting the Limits of Integration
If you’re evaluating a definite integral, remember to change the limits of integration to reflect the new variable u. Substitute the original limits into the substitution equation u = g(x) to find the new limits.
4. Evaluating the New Integral
Evaluate the simplified integral with respect to u. This should be a more straightforward integral that you can solve using standard integration techniques.
5. Converting Back to the Original Variable (if necessary)
If you’re evaluating an indefinite integral, you’ll need to convert back to the original variable x after integrating. Substitute g(x) back in for u to express the final answer in terms of x.
Alternative Approaches and Considerations
While the substitution method is effective for the given integral, it’s important to be aware of alternative approaches and considerations that might be useful in different scenarios.
1. Recognizing Standard Forms
Sometimes, integrals can be simplified by recognizing standard integral forms. For example, if you encounter an integral of the form ∫ f'(x) / f(x) dx, you can immediately recognize that the answer is ln|f(x)| + C.
2. Simplifying the Integrand Algebraically
Before attempting any integration technique, it’s often helpful to simplify the integrand algebraically. This might involve expanding expressions, combining terms, or using trigonometric identities to rewrite the integrand in a more manageable form.
3. Checking Your Work
After evaluating an integral, it’s always a good idea to check your work by differentiating the result. If you differentiate your answer and obtain the original integrand, you can be confident that your integration is correct.
Conclusion
Evaluating the definite integral ∫[1 to 2] e^(1/x^4) / x^5 dx involves careful application of the substitution method, accurate computation, and attention to detail. By following the step-by-step solution outlined in this article and avoiding common mistakes, you can successfully tackle similar integration problems. Additionally, understanding other integration techniques and being aware of alternative approaches can broaden your problem-solving skills and enable you to handle more complex integrals. Remember, practice is key to mastering these concepts and becoming proficient in calculus.
Latest Posts
Latest Posts
-
Mass Extinctions Create Conditions That Promote
Nov 27, 2025
-
Which Of The Following M And A Transaction Equations Is Correct
Nov 27, 2025
-
Which Of The Following Determines Lung Compliance
Nov 27, 2025
-
Knuckle Like Process At The End Of A Bone
Nov 27, 2025
-
Select The Correct Statement About Lymph Transport
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Definite Integral. 2 E 1/x4 X5 Dx 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.