Evaluate The Integral 4 1 X Dx
arrobajuarez
Nov 22, 2025 · 8 min read
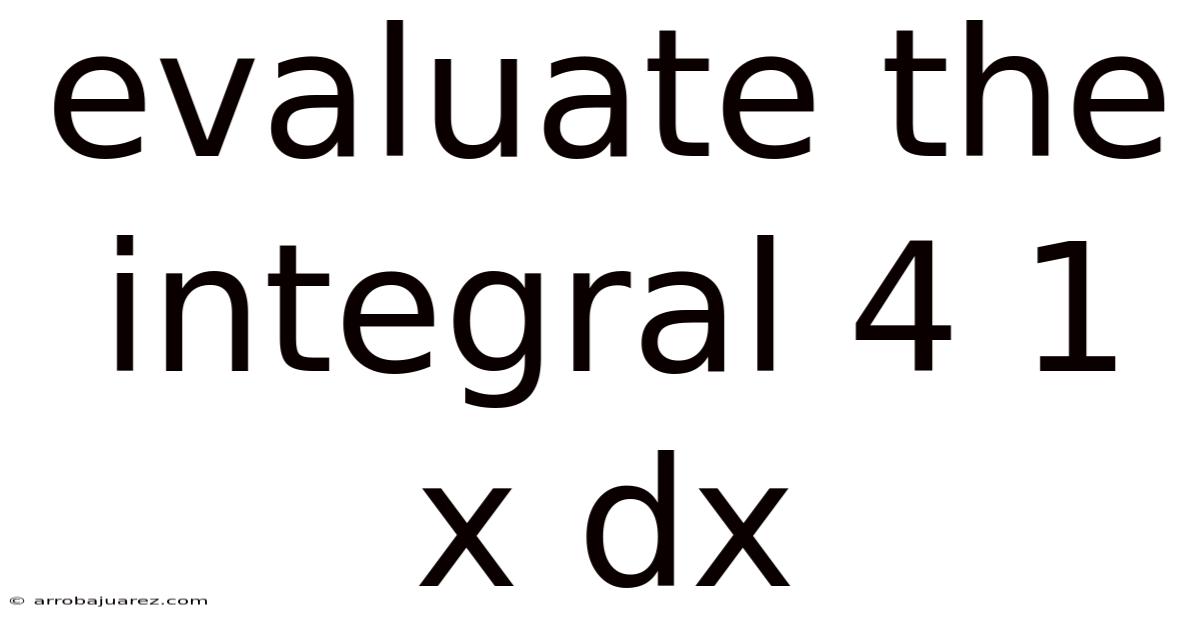
Table of Contents
Evaluating the definite integral ∫41 x dx involves finding the area under the curve of the function f(x) = x from x = 1 to x = 4. This article will guide you through the process step-by-step, explain the underlying mathematical principles, provide visual aids, and address common questions related to this type of calculation.
Understanding the Definite Integral
The definite integral ∫ab f(x) dx represents the signed area between the curve f(x) and the x-axis from x = a to x = b. In simpler terms, it's the accumulation of the function's values over the interval [a, b]. When f(x) is positive, the integral represents the actual area. When f(x) is negative, the integral represents the negative of the area.
For our integral ∫41 x dx, f(x) = x, a = 1, and b = 4. This means we are finding the area under the line y = x from x = 1 to x = 4.
Steps to Evaluate the Integral ∫41 x dx
Here's a breakdown of the steps to evaluate the integral:
- Find the Antiderivative: Determine the antiderivative (indefinite integral) of the function f(x) = x.
- Apply the Fundamental Theorem of Calculus: Evaluate the antiderivative at the upper and lower limits of integration (x = 4 and x = 1, respectively).
- Subtract: Subtract the value of the antiderivative at the lower limit from the value at the upper limit.
Let's proceed with each step in detail.
Step 1: Find the Antiderivative
The antiderivative of a function f(x) is a function F(x) such that F'(x) = f(x). In other words, it's the reverse process of differentiation.
For f(x) = x, we need to find a function whose derivative is x. Using the power rule of integration, which states ∫xn dx = (xn+1)/(n+1) + C (where C is the constant of integration), we get:
∫x dx = ∫x1 dx = (x1+1)/(1+1) + C = (x2)/2 + C
Therefore, the antiderivative of x is (x2)/2 + C. We can ignore the constant of integration, C, when evaluating definite integrals because it will cancel out in the subtraction step.
Step 2: Apply the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus provides a direct link between differentiation and integration. It states that if F(x) is an antiderivative of f(x), then:
∫ab f(x) dx = F(b) - F(a)
In our case, F(x) = (x2)/2, a = 1, and b = 4. We need to evaluate F(4) and F(1).
- F(4) = (42)/2 = 16/2 = 8
- F(1) = (12)/2 = 1/2
Step 3: Subtract
Finally, we subtract the value of the antiderivative at the lower limit from the value at the upper limit:
∫41 x dx = F(4) - F(1) = 8 - 1/2 = 16/2 - 1/2 = 15/2 = 7.5
Therefore, the value of the definite integral ∫41 x dx is 7.5.
Visualizing the Integral
The integral ∫41 x dx represents the area under the line y = x from x = 1 to x = 4. This area can be visualized as a trapezoid. The height of the trapezoid is the interval width (4 - 1 = 3), and the parallel sides are the function values at x = 1 and x = 4.
- At x = 1, y = x = 1
- At x = 4, y = x = 4
The area of a trapezoid is given by:
Area = (1/2) * (sum of parallel sides) * height
Area = (1/2) * (1 + 4) * 3 = (1/2) * 5 * 3 = 15/2 = 7.5
This confirms our calculated value of the integral. The area under the curve y = x from x = 1 to x = 4 is indeed 7.5 square units.
Why This Works: A More Detailed Explanation
The Fundamental Theorem of Calculus is the cornerstone of this calculation. To understand why it works, let's briefly revisit the concept of Riemann sums.
The definite integral is fundamentally a limit of a sum. Imagine dividing the interval [1, 4] into n small subintervals, each of width Δx. Within each subinterval, we can choose a point xi. The area of the rectangle with width Δx and height f(xi) is f(xi)Δx.
The Riemann sum is the sum of all these rectangular areas:
∑i=1n f(xi)Δx
As n approaches infinity (and Δx approaches zero), this sum approaches the definite integral:
∫ab f(x) dx = limn→∞ ∑i=1n f(xi)Δx
The beauty of the Fundamental Theorem is that it provides a much easier way to calculate this limit. It connects the concept of accumulation (the integral) with the concept of rate of change (the derivative).
Essentially, the antiderivative F(x) represents the accumulated area up to a point x. When we evaluate F(b) - F(a), we are finding the difference in accumulated area between x = b and x = a, which is precisely the area under the curve from a to b. The constant of integration, C, is irrelevant because it cancels out in the subtraction.
Common Mistakes and How to Avoid Them
- Forgetting the Antiderivative: The most common mistake is attempting to evaluate the function directly without finding the antiderivative first. Remember that integration is the reverse of differentiation, and the antiderivative is crucial.
- Incorrectly Applying the Power Rule: Ensure you correctly apply the power rule of integration. ∫xn dx = (xn+1)/(n+1) + C. Don't forget to add 1 to the exponent and divide by the new exponent.
- Reversing the Limits of Integration: Subtract the value of the antiderivative at the lower limit from the value at the upper limit. Reversing this order will result in a sign error.
- Ignoring the Constant of Integration (in Indefinite Integrals): While the constant of integration cancels out in definite integrals, it is essential for indefinite integrals. Omitting it can lead to incomplete or incorrect solutions.
Further Exploration: More Complex Integrals
The integral ∫41 x dx is a relatively simple example. However, the principles remain the same for more complex integrals. Consider these examples:
- ∫41 x2 dx: The antiderivative of x2 is (x3)/3. Therefore, the integral evaluates to [(43)/3] - [(13)/3] = 64/3 - 1/3 = 63/3 = 21.
- ∫41 (2x + 3) dx: The antiderivative of (2x + 3) is x2 + 3x. Therefore, the integral evaluates to [(42 + 34)] - [(12 + 31)] = (16 + 12) - (1 + 3) = 28 - 4 = 24.
- ∫41 √x dx: The antiderivative of √x (which is x1/2) is (2/3)x3/2. Therefore, the integral evaluates to [(2/3)(4)3/2] - [(2/3)(1)3/2] = (2/3)(8) - (2/3)(1) = 16/3 - 2/3 = 14/3.
These examples demonstrate that the fundamental process of finding the antiderivative and applying the Fundamental Theorem of Calculus remains consistent, regardless of the complexity of the function.
Applications of Definite Integrals
Definite integrals have numerous applications in various fields, including:
- Physics: Calculating displacement, work done by a force, and the center of mass.
- Engineering: Determining areas, volumes, and moments of inertia for structural design.
- Economics: Calculating consumer surplus and producer surplus.
- Statistics: Finding probabilities and expected values.
- Computer Science: Implementing numerical integration methods for solving complex equations.
Understanding definite integrals is crucial for solving many real-world problems. They provide a powerful tool for quantifying accumulated quantities and understanding rates of change.
Using Technology to Evaluate Integrals
While it's essential to understand the manual process of evaluating integrals, technology can be a valuable tool for verifying your results and handling more complex integrals. Many calculators and software packages can compute definite integrals, including:
- Online Integral Calculators: Websites like Wolfram Alpha and Symbolab offer free integral calculators.
- Scientific Calculators: Many scientific calculators have built-in integration functions.
- Mathematical Software: Software packages like MATLAB, Mathematica, and Maple provide comprehensive tools for symbolic and numerical computation, including integration.
- Programming Languages: Libraries in languages like Python (e.g., SciPy) can be used for numerical integration.
When using these tools, make sure you understand the syntax and input requirements. Double-check your inputs to avoid errors. Technology should be used as a supplement to your understanding, not a replacement for it.
Key Takeaways
- The definite integral ∫ab f(x) dx represents the signed area under the curve f(x) from x = a to x = b.
- The Fundamental Theorem of Calculus provides a direct link between differentiation and integration.
- To evaluate a definite integral, find the antiderivative of the function, evaluate it at the upper and lower limits of integration, and subtract.
- Visualizing the integral can help you understand its geometric meaning.
- Definite integrals have numerous applications in various fields.
- Technology can be used to verify your results and handle more complex integrals.
Conclusion
Evaluating the integral ∫41 x dx demonstrates the fundamental principles of definite integration. By understanding the concept of the antiderivative, applying the Fundamental Theorem of Calculus, and visualizing the integral, you can confidently tackle more complex integration problems. This skill is essential for various applications in science, engineering, and mathematics. Remember to practice and utilize available resources to strengthen your understanding. This knowledge will undoubtedly prove invaluable in your future academic and professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about Evaluate The Integral 4 1 X Dx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.