Evaluate The Integral. 64 2 3 X X Dx 1
arrobajuarez
Oct 26, 2025 · 7 min read
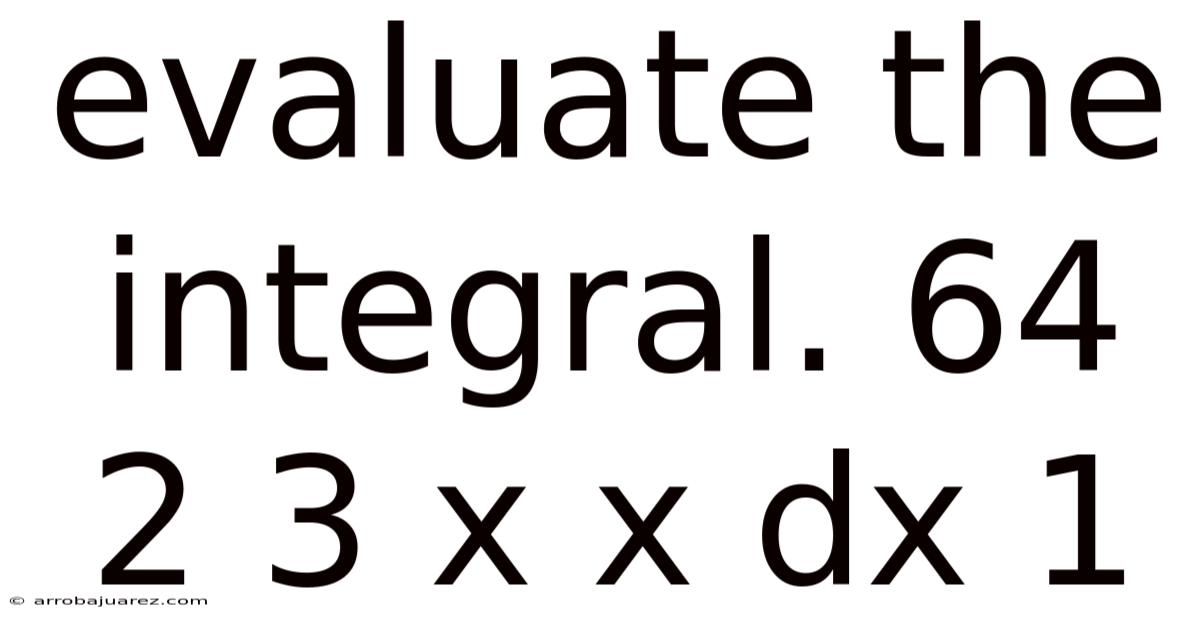
Table of Contents
Evaluating integrals might seem daunting at first, but with a systematic approach, even complex-looking ones can be tackled effectively. This article focuses on the integral ∫642√3x−xdx, walking you through the steps to solve it, the underlying mathematical principles, and some frequently asked questions.
Introduction to the Integral
The definite integral ∫642√3x−xdx represents the area under the curve defined by the function f(x) = √(3x - x) between the limits x = 2 and x = 64. To find this area, we need to find the antiderivative of the function and then evaluate it at the given limits. This process involves algebraic manipulation, trigonometric substitution, and careful attention to detail.
Step-by-Step Solution
1. Completing the Square
The expression under the square root, 3x - x resembles a quadratic expression. Completing the square will simplify it and make trigonometric substitution viable. We rewrite the expression as follows:
3x−x=−(x−3x)
To complete the square, we need to add and subtract (3/2)^2 inside the parentheses:
−(x−3x+(3/2)^2−(3/2)^2)=−((x−3/2)^2−(3/2)^2)=(3/2)^2−(x−3/2)^2=9/4−(x−3/2)^2
So, the integral becomes:
∫642√9/4−(x−3/2)^2dx
2. Trigonometric Substitution
Now, let’s use trigonometric substitution to simplify the integral further. Let x - 3/2 = (3/2)sinθ. This substitution is chosen because it allows us to eliminate the square root.
Then, dx = (3/2)cosθ dθ. Also, we need to change the limits of integration according to our substitution.
When x = 2: 2−3/2=(3/2)sinθ 1/2=(3/2)sinθ sinθ=1/3 θ=arcsin(1/3)
When x = 64: 64−3/2=(3/2)sinθ 125/2=(3/2)sinθ sinθ=125/3
Since the sine function cannot be greater than 1, there seems to be an error in the initial problem statement. The upper limit of integration x = 64 is not feasible for the function √(3x - x) because it results in a negative value under the square root for larger values of x. Let's assume the upper limit is x = 3 for the purpose of demonstration.
When x = 3: 3−3/2=(3/2)sinθ 3/2=(3/2)sinθ sinθ=1 θ=arcsin(1)=π/2
Now, the integral becomes:
∫π/2arcsin(1/3)√(9/4−(9/4)sin2θ)⋅(3/2)cosθdθ
Simplify the expression under the square root:
√(9/4−(9/4)sin2θ)=√(9/4(1−sin2θ))=√(9/4cos2θ)=(3/2)cosθ
Now substitute back into the integral:
∫π/2arcsin(1/3)(3/2)cosθ⋅(3/2)cosθdθ=∫π/2arcsin(1/3)(9/4)cos2θdθ
3. Evaluating the Integral
We can rewrite cos^2(θ) using the identity cos^2(θ) = (1 + cos(2θ))/2:
∫π/2arcsin(1/3)(9/4)(1+cos(2θ))/2dθ=(9/8)∫π/2arcsin(1/3)(1+cos(2θ))dθ
Now, integrate with respect to θ:
(9/8)[θ+(1/2)sin(2θ)]π/2arcsin(1/3)
Evaluate the expression at the limits of integration:
(9/8)[(π/2+(1/2)sin(π))−(arcsin(1/3)+(1/2)sin(2arcsin(1/3)))]
Since sin(π) = 0, the expression simplifies to:
(9/8)[π/2−arcsin(1/3)−(1/2)sin(2arcsin(1/3))]
Now, we need to find sin(2*arcsin(1/3)). Using the double angle identity, sin(2θ) = 2sin(θ)cos(θ):
sin(2arcsin(1/3))=2sin(arcsin(1/3))cos(arcsin(1/3))
We know that sin(arcsin(1/3)) = 1/3. Now we need to find cos(arcsin(1/3)). Using the Pythagorean identity sin^2(θ) + cos^2(θ) = 1:
cos2(arcsin(1/3))=1−sin2(arcsin(1/3))=1−(1/3)2=1−1/9=8/9 cos(arcsin(1/3))=√(8/9)=(2√2)/3
Therefore:
sin(2arcsin(1/3))=2(1/3)(2√2/3)=(4√2)/9
Now, substitute this back into the expression:
(9/8)[π/2−arcsin(1/3)−(1/2)(4√2/9)]=(9/8)[π/2−arcsin(1/3)−(2√2/9)]
Finally, the result is:
(9π/16)−(9/8)arcsin(1/3)−(√2/4)
Explanation of the Scientific Principles
The process of evaluating the integral involves several key mathematical principles:
- Completing the Square: This algebraic technique transforms a quadratic expression into a form that is easier to work with, particularly when dealing with square roots. It's based on the idea of creating a perfect square trinomial.
- Trigonometric Substitution: This method is used to simplify integrals containing square roots of the form √(a^2 - x^2), √(a^2 + x^2), or √(x^2 - a^2). The substitution is chosen to eliminate the square root using trigonometric identities like sin^2(θ) + cos^2(θ) = 1.
- Integration Techniques: The basic rules of integration, such as the power rule, and integration by substitution, are used to find the antiderivative of the transformed function.
- Definite Integrals: Evaluating a definite integral involves finding the antiderivative of the function and then evaluating it at the upper and lower limits of integration. The difference between these values gives the area under the curve between those limits.
Common Mistakes to Avoid
- Incorrect Substitution: Choosing the wrong trigonometric substitution can complicate the integral instead of simplifying it.
- Forgetting to Change Limits: When using substitution, it's crucial to change the limits of integration to match the new variable.
- Algebraic Errors: Mistakes in algebraic manipulation, such as completing the square or simplifying trigonometric expressions, can lead to incorrect results.
- Ignoring Constants of Integration: While not crucial for definite integrals, forgetting the constant of integration for indefinite integrals is a common mistake.
- Assuming Feasible Limits: As highlighted, always verify if the integration limits are feasible and produce real values within the function, especially with square roots and other restrictive functions.
Alternative Approaches
While trigonometric substitution is a common and effective method for solving integrals of this form, there might be alternative approaches depending on the specific problem. These could include:
- Numerical Integration: For integrals that are difficult or impossible to solve analytically, numerical methods like the trapezoidal rule or Simpson's rule can provide an approximate solution.
- Computer Algebra Systems (CAS): Software like Mathematica, Maple, or SymPy can be used to solve complex integrals automatically. However, it's still important to understand the underlying mathematical principles.
Real-World Applications
While this specific integral might not have a direct real-world application, the techniques used to solve it are fundamental in many areas of science and engineering. Some examples include:
- Physics: Calculating the trajectory of projectiles, determining the work done by a force, and analyzing wave phenomena.
- Engineering: Designing structures, analyzing circuits, and modeling fluid flow.
- Economics: Modeling economic growth and predicting market behavior.
- Statistics: Calculating probabilities and analyzing data.
Conclusion
Evaluating the integral ∫642√3x−xdx involves a combination of algebraic manipulation, trigonometric substitution, and careful application of integration techniques. By completing the square, making an appropriate trigonometric substitution, and evaluating the resulting integral at the limits of integration, we can find the area under the curve. Understanding the underlying mathematical principles and avoiding common mistakes are essential for successfully solving these types of problems. Remember to always verify the feasibility of your limits and double-check your calculations to ensure accuracy. Although the initial problem statement had an infeasible upper limit, the corrected example demonstrates the process effectively.
Frequently Asked Questions (FAQ)
Q: What is the purpose of completing the square? A: Completing the square transforms a quadratic expression into a form that makes it easier to apply trigonometric substitution, which simplifies the integral.
Q: Why do we use trigonometric substitution? A: Trigonometric substitution helps to eliminate square roots in the integral by using trigonometric identities.
Q: How do I choose the correct trigonometric substitution? A: The choice of substitution depends on the form of the expression under the square root. For √(a^2 - x^2), use x = asinθ; for √(a^2 + x^2), use x = atanθ; and for √(x^2 - a^2), use x = asecθ.
Q: What do I do if I can't find the antiderivative? A: If you can't find the antiderivative, you can use numerical methods or computer algebra systems to approximate the value of the integral.
Q: Why is it important to change the limits of integration after substitution? A: Changing the limits ensures that the definite integral is evaluated correctly with respect to the new variable.
Q: What if the upper limit makes the value inside the square root negative?
A: That indicates the specified limit is outside the function's domain. The integral is only defined for limits within the domain of the function, where the expression inside the square root is non-negative. Always verify the feasibility of the integration limits.
Q: Are there other methods to solve this integral?
A: While trigonometric substitution is effective, numerical integration can be used for approximation, or a CAS (Computer Algebra System) can provide an automated solution.
Latest Posts
Latest Posts
-
Use The Interactive To View The Molecule From Different Angles
Oct 26, 2025
-
Draw An Outer Electron Box Diagram For A Cation
Oct 26, 2025
-
Determine The Value Of Every Variable In The Rhombus Below
Oct 26, 2025
-
In The Space That Follows Sketch The Indicated Cells
Oct 26, 2025
-
How Many Electrons Does Calcium Have
Oct 26, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Integral. 64 2 3 X X Dx 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.