Five And Twenty-two Thousandths As A Decimal
arrobajuarez
Dec 02, 2025 · 8 min read
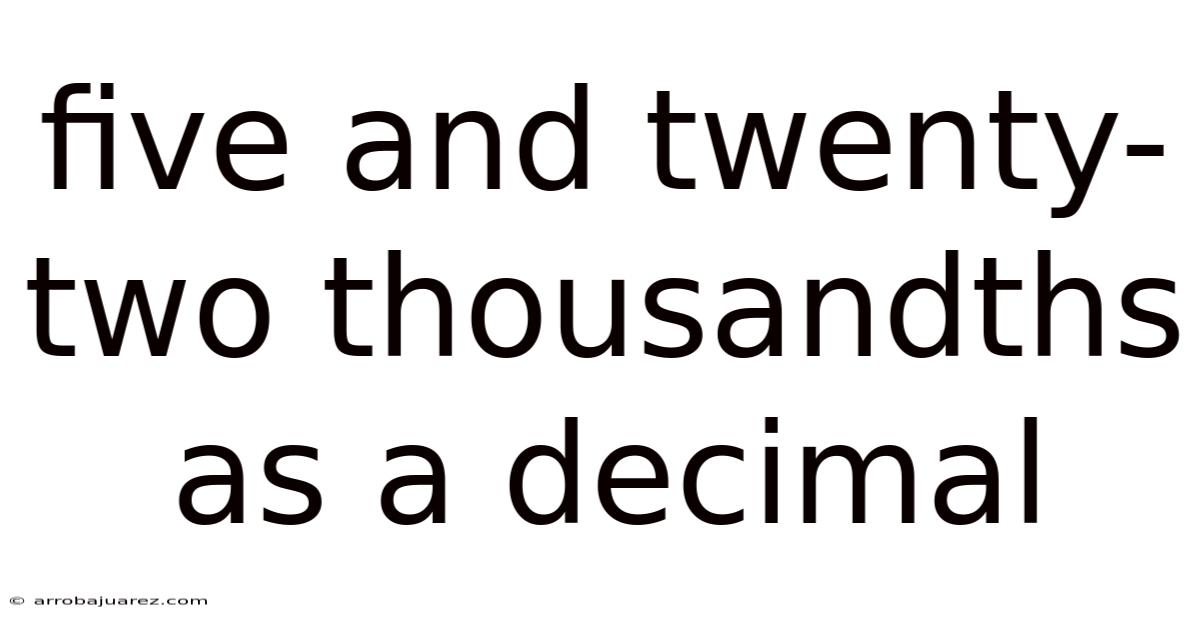
Table of Contents
Five and twenty-two thousandths sounds like a complex number, but it's simply a matter of understanding place value. Converting this phrase into a decimal is a fundamental skill in mathematics with real-world applications in fields like finance, science, and engineering. Understanding how to accurately represent numbers like "five and twenty-two thousandths" as a decimal ensures precise calculations and clear communication of quantities. This article will break down the process step-by-step, ensuring clarity and accuracy.
Understanding Place Value: The Foundation of Decimals
Before converting "five and twenty-two thousandths" to a decimal, it’s crucial to grasp the concept of place value. The decimal system is a base-10 system, meaning each digit in a number represents a power of 10.
To the left of the decimal point, we have:
- Ones: 10⁰ = 1
- Tens: 10¹ = 10
- Hundreds: 10² = 100
- Thousands: 10³ = 1000
- And so on...
To the right of the decimal point, we have:
- Tenths: 10⁻¹ = 0.1
- Hundredths: 10⁻² = 0.01
- Thousandths: 10⁻³ = 0.001
- Ten-thousandths: 10⁻⁴ = 0.0001
- And so on...
Understanding these place values is essential for accurately converting word form numbers into their decimal equivalents.
Breaking Down "Five and Twenty-Two Thousandths"
Now that we understand place value, let's dissect the phrase "five and twenty-two thousandths." This phrase can be broken down into two distinct parts:
- "Five": This refers to the whole number part of the decimal.
- "And twenty-two thousandths": This refers to the fractional part of the decimal.
The word "and" typically signifies the decimal point, separating the whole number from the fractional part. The phrase "twenty-two thousandths" indicates that we are dealing with a value that extends to the thousandths place.
Step-by-Step Conversion to Decimal Form
Let's convert "five and twenty-two thousandths" into a decimal, step-by-step:
- Identify the Whole Number: The whole number is "five," which we write as 5.
- Place the Decimal Point: Since we have a whole number and a fractional part, we place a decimal point after the whole number: 5.
- Determine the Fractional Part: We have "twenty-two thousandths." This means we need to represent 22 in the thousandths place.
- Write the Fractional Part: To represent 22 in the thousandths place, we write it as 022. This is because the thousandths place is three positions to the right of the decimal point.
- Combine the Parts: Combine the whole number and the fractional part to get the final decimal: 5.022
Therefore, "five and twenty-two thousandths" as a decimal is 5.022.
Common Mistakes to Avoid
Converting word form numbers to decimals can be tricky, and certain common mistakes can lead to errors. Here are some pitfalls to watch out for:
- Misinterpreting "And": The word "and" usually indicates the position of the decimal point. Avoid placing "and" anywhere else in the number.
- Incorrect Place Value: Ensure that the digits in the fractional part are placed in the correct place values. For instance, "twenty-two thousandths" requires the digits to extend to the thousandths place.
- Forgetting Placeholder Zeros: If the fractional part does not fill all the places to the right of the decimal point, you must use placeholder zeros to maintain correct place value.
- Reading the Number Incorrectly: Always read the word form number carefully to understand its components. Misreading the number can lead to an incorrect conversion.
By avoiding these common mistakes, you can ensure accurate conversions every time.
Examples and Practice
To solidify your understanding, let's look at some examples and practice converting similar phrases into decimal form:
Example 1: Three and forty-five hundredths
- Whole number: 3
- Fractional part: forty-five hundredths (0.45)
- Decimal form: 3.45
Example 2: Ten and seven thousandths
- Whole number: 10
- Fractional part: seven thousandths (0.007)
- Decimal form: 10.007
Example 3: One hundred and one tenth
- Whole number: 100
- Fractional part: one tenth (0.1)
- Decimal form: 100.1
Now, try converting these phrases on your own:
- Six and twelve thousandths
- Twenty-five and three hundredths
- One and five ten-thousandths
Check your answers:
- 6.012
- 25.03
- 1.0005
Real-World Applications
Understanding how to convert phrases like "five and twenty-two thousandths" into decimals is not just an academic exercise. It has practical applications in various fields:
- Finance: In finance, decimals are used to represent monetary values, interest rates, and investment returns. Accurately converting values is essential for financial transactions and reporting.
- Science: Scientists use decimals to represent measurements, experimental data, and constants. Precision in decimal representation is crucial for accurate scientific analysis.
- Engineering: Engineers rely on decimals for precise measurements, calculations, and specifications in design and construction.
- Everyday Life: Decimals are encountered in everyday situations such as shopping, cooking, and measuring. Understanding decimals helps in making informed decisions and accurate calculations.
The Significance of Precision
The accuracy of decimal representation is of paramount importance in many applications. Even small errors in decimal values can lead to significant discrepancies.
In finance, for instance, an incorrect decimal representation can result in miscalculation of interest, incorrect pricing, or inaccurate financial statements. In science and engineering, precision is vital for reliable experimental results, accurate models, and safe designs.
Therefore, it is crucial to pay attention to detail and ensure that decimal values are converted and represented accurately.
Advanced Concepts: Rounding and Significant Figures
Once you are comfortable converting phrases to decimals, it's beneficial to understand related concepts such as rounding and significant figures.
-
Rounding: Rounding involves approximating a decimal value to a certain number of decimal places. The rules for rounding are as follows:
- If the digit to the right of the rounding place is 5 or greater, round up.
- If the digit to the right of the rounding place is less than 5, round down.
-
Significant Figures: Significant figures indicate the precision of a decimal value. They include all non-zero digits and any zeros between non-zero digits or that are trailing zeros in a number with a decimal point.
Understanding these concepts can help you work with decimals more effectively and communicate numerical information accurately.
Tips for Mastering Decimal Conversions
To become proficient at converting phrases to decimals, consider these tips:
- Practice Regularly: Consistent practice is key to mastering decimal conversions.
- Understand Place Value: Reinforce your understanding of place value and how it relates to decimals.
- Break Down Phrases: Break down complex phrases into smaller, more manageable parts.
- Use Visual Aids: Use visual aids such as place value charts to help you visualize decimal conversions.
- Check Your Work: Always check your work to ensure accuracy.
Frequently Asked Questions (FAQ)
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, divide the numerator (top number) by the denominator (bottom number). For example, to convert 1/4 to a decimal, divide 1 by 4, which equals 0.25.
Q: What is the difference between a decimal and a fraction?
A: A decimal is a number expressed in base-10 notation, using a decimal point to separate the whole number part from the fractional part. A fraction represents a part of a whole and is written as a ratio of two numbers (numerator and denominator).
Q: How do I round a decimal to the nearest tenth?
A: To round a decimal to the nearest tenth, look at the digit in the hundredths place. If it is 5 or greater, round up the tenths digit. If it is less than 5, leave the tenths digit as it is.
Q: How do I add or subtract decimals?
A: To add or subtract decimals, line up the decimal points and add or subtract the numbers as you would with whole numbers. Ensure that you carry over or borrow as needed, and place the decimal point in the answer in the same position as in the original numbers.
Q: What is a repeating decimal?
A: A repeating decimal is a decimal that has a repeating pattern of digits. For example, 1/3 = 0.333... (the 3 repeats indefinitely). Repeating decimals are often indicated by a bar over the repeating digits.
Q: How do I convert a repeating decimal to a fraction?
A: Converting a repeating decimal to a fraction involves algebraic manipulation. For example, to convert 0.333... to a fraction:
- Let x = 0.333...
- Multiply both sides by 10: 10x = 3.333...
- Subtract the original equation from the new equation: 10x - x = 3.333... - 0.333...
- Simplify: 9x = 3
- Solve for x: x = 3/9 = 1/3
Conclusion
Converting "five and twenty-two thousandths" to a decimal requires understanding place value and breaking down the phrase into its component parts. By following a step-by-step process and avoiding common mistakes, you can accurately convert any word form number into its decimal equivalent. This skill is essential for various real-world applications and contributes to precision and accuracy in calculations and communication. Mastering decimal conversions empowers you to handle numerical information with confidence and competence. Regular practice and a solid understanding of the underlying principles will make you a pro at converting phrases to decimals.
Latest Posts
Related Post
Thank you for visiting our website which covers about Five And Twenty-two Thousandths As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.