Pq 2x 1 And Qr 5x 44 Find Pq
arrobajuarez
Nov 17, 2025 · 10 min read
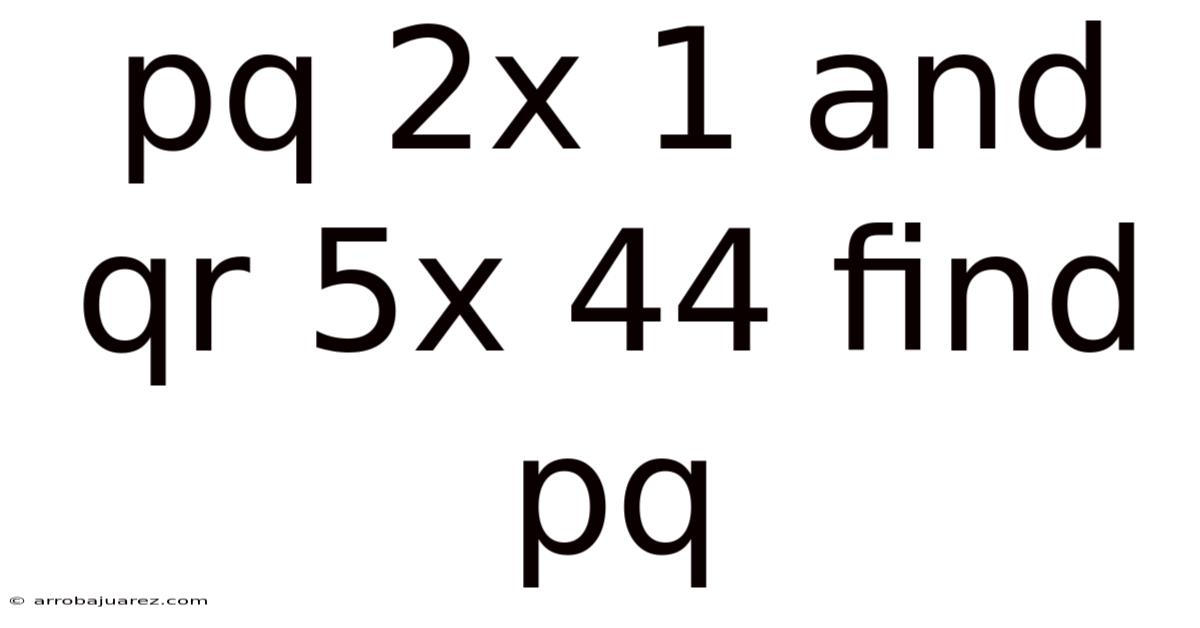
Table of Contents
Let's embark on a journey to solve this algebraic puzzle, unraveling the values of p, q, and ultimately, the expression pq. This exercise delves into the realms of simultaneous equations, requiring a blend of algebraic manipulation and logical deduction to arrive at the final solution.
Decoding the Equations: A Step-by-Step Approach
Our mission is to find the value of pq, given two equations:
- pq = 2x + 1
- qr = 5x + 44
These equations present a classic scenario where we need to find the individual values of the variables or manipulate the equations to directly find the value of the expression we are interested in (pq).
Step 1: Isolating 'x' in Both Equations
The first step towards solving these simultaneous equations involves isolating the variable x in both equations. This will allow us to equate the two expressions, effectively eliminating x and giving us a relationship between p, q, and r.
Equation 1: pq = 2x + 1
- Subtract 1 from both sides: pq - 1 = 2x
- Divide both sides by 2: (pq - 1) / 2 = x
Equation 2: qr = 5x + 44
- Subtract 44 from both sides: qr - 44 = 5x
- Divide both sides by 5: (qr - 44) / 5 = x
Now we have:
- x = (pq - 1) / 2
- x = (qr - 44) / 5
Step 2: Equating the Expressions for 'x'
Since both expressions are equal to x, we can set them equal to each other:
(pq - 1) / 2 = (qr - 44) / 5
This equation now relates p, q, and r without the presence of x.
Step 3: Eliminating the Fractions
To simplify the equation, we can eliminate the fractions by cross-multiplying:
5(pq - 1) = 2(qr - 44)
Expanding both sides of the equation, we get:
5pq - 5 = 2qr - 88
Step 4: Rearranging the Equation
Let's rearrange the equation to group similar terms and try to isolate pq:
5pq = 2qr - 88 + 5
5pq = 2qr - 83
Now we have an equation that expresses 5pq in terms of qr. This is a step forward, but we still need to find a way to isolate pq completely.
Step 5: The Importance of Additional Information
At this point, we encounter a challenge. The equation 5pq = 2qr - 83 contains three unknowns (p, q, and r) in a single equation. This means we need more information to solve for the unique value of pq. Without additional constraints or equations, there are infinitely many solutions for p, q, and r that would satisfy this equation.
Let's explore some possible scenarios and hypothetical information that could help us find a unique solution.
Scenario 1: Knowing the Value of 'r'
If we knew the value of r, we could substitute it into the equation and solve for pq. For example, let's say we are given that r = 1:
5pq = 2q(1) - 83
5pq = 2q - 83
Even with knowing 'r', we still have two unknowns (p and q) in a single equation. We can't directly solve for pq yet, but we can express p in terms of q:
5p = 2 - (83/q)
p = (2/5) - (83/5q)
Now, let's substitute r = 1 back into the original equation qr = 5x + 44:
q(1) = 5x + 44
q = 5x + 44
x = (q - 44)/5
Now, let's substitute x = (q-44)/5 into the original equation pq = 2x + 1:
pq = 2((q-44)/5) + 1
pq = (2q - 88)/5 + 1
pq = (2q - 88 + 5)/5
pq = (2q - 83)/5
This is the same equation we derived earlier: 5pq = 2q - 83. We still need another piece of information.
Scenario 2: Knowing the Relationship Between 'p' and 'r'
Suppose we know that p = r. Then we can substitute p for r in the equation 5pq = 2qr - 83:
5pq = 2qp - 83
5pq = 2pq - 83
Subtracting 2pq from both sides:
3pq = -83
pq = -83/3
In this scenario, knowing that p = r allows us to directly solve for pq.
Scenario 3: Knowing the Value of 'q'
If we are given the value of q, we can substitute it into the equation 5pq = 2qr - 83 and solve for pq. For example, let's assume q = 1.
5pq = 2(1)*r - 83
5pq = 2*r - 83
We still need more information. Let's revisit the original equations and substitute q = 1.
p(1) = 2x + 1 => p = 2x + 1 (1)r = 5x + 44 => r = 5x + 44
We still have three unknowns, p, r, and x.
Key Takeaway: To find a unique numerical value for pq, we must have additional information beyond the two initial equations. This information could take the form of:
- The value of r.
- A direct relationship between p, q, and/or r (e.g., p = r, q = 2p, etc.).
- A third independent equation involving p, q, r, and/or x.
Step 6: Let's Assume a Value for 'x' to Illustrate a Complete Solution
Since we've established that we need more information, let's assume a value for x purely for illustrative purposes. This will allow us to demonstrate how to find pq if we had sufficient data.
Let's say x = -8.
Now we can use the original equations:
- pq = 2x + 1 = 2(-8) + 1 = -16 + 1 = -15
- qr = 5x + 44 = 5(-8) + 44 = -40 + 44 = 4
So, if x = -8, then pq = -15 and qr = 4. Let's see if we can find values for p, q, and r that satisfy these conditions.
Since pq = -15, we can say p = -15/q. Substituting into qr = 4, we get:
q*r = 4 => r = 4/q
Now let's use the equation derived earlier, 5pq = 2qr - 83
5(-15) = 2(4) - 83
-75 = 8 - 83
-75 = -75
This confirms that our assumed value of x = -8 leads to a consistent system of equations with pq = -15.
Now, let's find possible values for p, q, and r. Since pq = -15, some possible pairs for (p, q) are: (1, -15), (-1, 15), (3, -5), (-3, 5), (5, -3), (-5, 3), (15, -1), (-15, 1).
Since qr = 4, some possible pairs for (q, r) are: (1, 4), (-1, -4), (2, 2), (-2, -2), (4, 1), (-4, -1).
We need to find a value of q that appears in both sets of pairs.
- If q = 1, then p = -15 and r = 4.
- If q = -1, then p = 15 and r = -4.
Therefore, one possible solution is: p = -15, q = 1, r = 4, and x = -8. Another possible solution is: p = 15, q = -1, r = -4, and x = -8.
Important Note: This solution is only valid because we assumed a value for x. Without that assumption (or other additional information), we cannot determine a unique value for pq.
The Underlying Mathematical Principles
This problem hinges on the fundamental principles of algebra, specifically:
- Simultaneous Equations: We are given two equations with multiple unknowns, requiring us to find values that satisfy both equations simultaneously.
- Substitution: A key technique used is substitution, where we solve one equation for one variable and substitute that expression into another equation. This allows us to reduce the number of unknowns in an equation.
- Algebraic Manipulation: We employ various algebraic operations (addition, subtraction, multiplication, division) to isolate variables and simplify equations.
- The Importance of Independent Equations: To solve for n unknowns, we generally need n independent equations. In our case, we had four unknowns (p, q, r, and x) but only two equations initially. This is why we needed additional information to find a unique solution.
Common Pitfalls to Avoid
When tackling problems like this, it's easy to make mistakes. Here are some common pitfalls to watch out for:
- Arithmetic Errors: Double-check your calculations, especially when dealing with negative numbers or fractions. A simple arithmetic error can throw off the entire solution.
- Incorrectly Applying Algebraic Operations: Ensure you are performing the same operation on both sides of the equation to maintain equality. For example, if you subtract a term from one side, you must subtract the same term from the other side.
- Forgetting to Distribute: When multiplying a number by an expression in parentheses, remember to distribute the number to each term inside the parentheses. For example, 2(qr - 44) = 2qr - 88, not 2qr - 44.
- Making Assumptions Without Justification: Be careful not to make assumptions about the values of variables unless you have solid evidence to support those assumptions. As we demonstrated, assuming a value for x allowed us to find a solution, but that solution was contingent on that assumption.
- Not Recognizing the Need for More Information: If you find yourself stuck with more unknowns than equations, recognize that you likely need additional information to solve the problem. Don't keep spinning your wheels trying to solve the unsolvable.
Frequently Asked Questions (FAQ)
Q: Why can't I solve for pq directly from the given equations?
A: You can't solve for a unique value of pq directly because you have more unknowns than independent equations. You need additional information, such as the value of r or a relationship between p, q, and r.
Q: What does it mean to have "more unknowns than equations"?
A: It means that there are infinitely many possible solutions that satisfy the given equations. Each variable can take on a range of values, and there isn't enough information to narrow down those values to a single, unique solution.
Q: Is there a way to find possible values for pq without knowing r or a relationship between the variables?
A: Yes, you can express pq in terms of qr (as we did in Step 4: 5pq = 2qr - 83). However, this doesn't give you a numerical value for pq; it only relates it to qr. You would still need to know the value of qr (or q and r individually) to calculate pq.
Q: What if the problem stated that p, q, and r are integers? Would that help?
A: Yes, if p, q, and r are integers, it would significantly narrow down the possible solutions. Knowing that the variables are integers imposes constraints that can help you find a unique solution or a limited set of possible solutions. You would need to test different integer values to see which ones satisfy the equations.
Q: If I encounter a similar problem, what should be my first steps?
A: 1. Clearly identify the unknowns and the equations. 2. Try to isolate variables and substitute expressions to reduce the number of unknowns in each equation. 3. If you find yourself with more unknowns than equations, recognize that you need additional information. 4. Look for any hidden relationships or constraints (e.g., the variables are integers, two variables are equal, etc.). 5. If you are given multiple-choice answers, try plugging those answers back into the original equations to see if they work.
Conclusion: The Power of Context and Additional Information
While the initial problem statement pq = 2x + 1 and qr = 5x + 44 doesn't provide enough information to directly calculate pq, it serves as a valuable exercise in algebraic manipulation and problem-solving. We learned how to isolate variables, equate expressions, and recognize the importance of having a sufficient number of independent equations to solve for multiple unknowns. The journey to finding pq highlighted the crucial role that additional information, such as knowing the value of r or the relationship between p and r, plays in arriving at a definitive solution. Remember, in mathematics, as in life, context and complete information are often key to unlocking the answers we seek. The ability to recognize when more data is needed is just as important as the algebraic skills themselves.
Latest Posts
Related Post
Thank you for visiting our website which covers about Pq 2x 1 And Qr 5x 44 Find Pq . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.