Pq 3x 14 And Qr 7x 10 Find X
arrobajuarez
Nov 02, 2025 · 9 min read
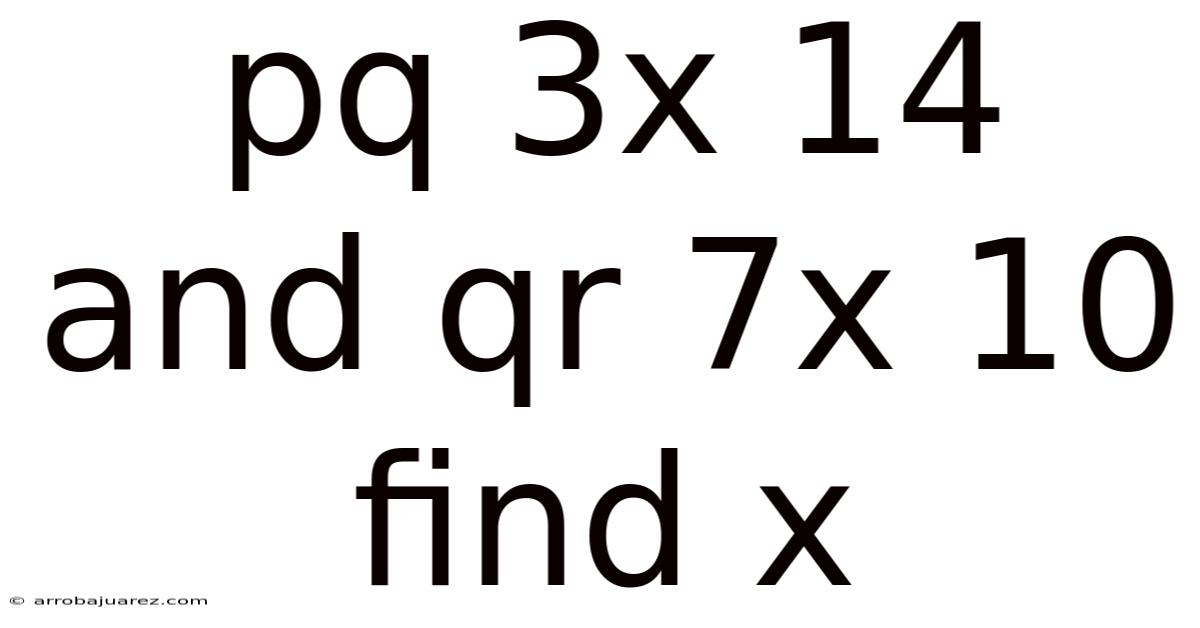
Table of Contents
Solving for 'x' in PQ 3x-14 and QR 7x-10: A Comprehensive Guide
The challenge of finding the value of 'x' when presented with expressions like PQ 3x-14 and QR 7x-10 often arises in geometry and algebra. These expressions usually represent the lengths of line segments, and the problem often hinges on understanding relationships between these segments. This article provides a comprehensive guide to understanding these types of problems, exploring various geometric relationships that might be implied, and outlining the algebraic steps needed to solve for 'x'.
Understanding the Problem: Line Segments and Relationships
Expressions like "PQ 3x-14" and "QR 7x-10" describe the lengths of line segments PQ and QR, respectively. The variable 'x' is an unknown quantity that influences the length of both segments. To find the value of 'x', we need additional information that relates PQ and QR. This information typically comes in the form of geometric relationships. Common relationships include:
- Congruence: PQ and QR are congruent (equal in length). This is often indicated by PQ ≅ QR or by stating "PQ is congruent to QR".
- Collinearity and Segment Addition: Points P, Q, and R are collinear (lie on the same line), and Q lies between P and R. In this case, PR = PQ + QR. We might be given an expression for PR.
- Ratio: The ratio of PQ to QR is a specific value (e.g., PQ is twice the length of QR).
- Similarity: PQ and QR are corresponding sides of similar triangles. This introduces a proportion involving other sides of the triangles.
Let's examine each of these scenarios and demonstrate how to solve for 'x' in each case.
Scenario 1: Congruent Segments (PQ ≅ QR)
This is the most straightforward scenario. If PQ and QR are congruent, their lengths are equal. Therefore:
PQ = QR
Substitute the given expressions:
3x - 14 = 7x - 10
Now, we solve for 'x' using basic algebra:
-
Isolate 'x' terms: Subtract 3x from both sides:
-14 = 4x - 10
-
Isolate the constant terms: Add 10 to both sides:
-4 = 4x
-
Solve for 'x': Divide both sides by 4:
x = -1
Important Consideration: Always check your solution by plugging the value of 'x' back into the original expressions for PQ and QR. In this case:
PQ = 3(-1) - 14 = -3 - 14 = -17
QR = 7(-1) - 10 = -7 - 10 = -17
Since lengths cannot be negative, this solution (x = -1) indicates that either:
- The problem is designed to explore algebraic manipulation without real-world geometric applicability.
- There is an error in the problem statement or the implied relationship.
In a real-world geometric context, negative lengths are impossible. Therefore, if you encounter a negative solution for 'x' that leads to negative lengths, carefully re-examine the problem statement and the assumed geometric relationships. There might be a subtle error or misunderstanding. Sometimes, the problem might be specifically designed to highlight this issue.
Scenario 2: Collinear Points and Segment Addition (P, Q, and R are collinear, Q is between P and R)
In this scenario, we know that the length of the entire segment PR is the sum of the lengths of its parts, PQ and QR:
PR = PQ + QR
We need an expression for PR to solve for 'x'. Let's assume PR is given as PR = 2x + 6. Then:
2x + 6 = (3x - 14) + (7x - 10)
Now, we solve for 'x':
-
Combine like terms on the right side:
2x + 6 = 10x - 24
-
Isolate 'x' terms: Subtract 2x from both sides:
6 = 8x - 24
-
Isolate the constant terms: Add 24 to both sides:
30 = 8x
-
Solve for 'x': Divide both sides by 8:
x = 30/8 = 15/4 = 3.75
Now, let's check our solution:
PQ = 3(3.75) - 14 = 11.25 - 14 = -2.75
QR = 7(3.75) - 10 = 26.25 - 10 = 16.25
PR = 2(3.75) + 6 = 7.5 + 6 = 13.5
Again, we encounter a negative length for PQ. This indicates a problem with the setup. The value of PR (2x + 6) might be incorrect or the points might not actually be collinear in the way described. It's crucial to examine the context of the problem.
Important Note: If the problem stated something like "Q is on line PR" instead of "Q is between P and R," then we couldn't assume segment addition. Q could be beyond R, making PR a part of PQ (or QR if Q were beyond P).
Scenario 3: Ratio of Segment Lengths (PQ is twice the length of QR)
If we are told that PQ is twice the length of QR, we can write:
PQ = 2 * QR
Substituting the given expressions:
3x - 14 = 2(7x - 10)
Now, we solve for 'x':
-
Distribute the 2 on the right side:
3x - 14 = 14x - 20
-
Isolate 'x' terms: Subtract 3x from both sides:
-14 = 11x - 20
-
Isolate the constant terms: Add 20 to both sides:
6 = 11x
-
Solve for 'x': Divide both sides by 11:
x = 6/11
Let's check the solution:
PQ = 3(6/11) - 14 = 18/11 - 154/11 = -136/11 (approximately -12.36)
QR = 7(6/11) - 10 = 42/11 - 110/11 = -68/11 (approximately -6.18)
Again, we have negative lengths. This reinforces the importance of checking solutions and interpreting them in the context of geometric reality. The ratio might be defined differently, or there may be an error in the problem statement.
Scenario 4: Similar Triangles and Proportions
Suppose PQ and QR represent corresponding sides of similar triangles. Let's say that PQ corresponds to side AB of triangle ABC, and QR corresponds to side DE of triangle DEF. Furthermore, suppose we know that AC = 4x + 2 and DF = 2x + 1. Because the triangles are similar, the ratios of corresponding sides are equal:
PQ/QR = AC/DF
Substituting the given expressions:
(3x - 14) / (7x - 10) = (4x + 2) / (2x + 1)
Now we have a proportion to solve:
-
Cross-multiply:
(3x - 14)(2x + 1) = (7x - 10)(4x + 2)
-
Expand both sides:
6x² + 3x - 28x - 14 = 28x² + 14x - 40x - 20
6x² - 25x - 14 = 28x² - 26x - 20
-
Move all terms to one side to set the equation to zero:
0 = 22x² - x - 6
-
Solve the quadratic equation. This can be done by factoring, completing the square, or using the quadratic formula:
x = (-b ± √(b² - 4ac)) / 2a
where a = 22, b = -1, and c = -6
x = (1 ± √((-1)² - 4 * 22 * -6)) / (2 * 22)
x = (1 ± √(1 + 528)) / 44
x = (1 ± √529) / 44
x = (1 ± 23) / 44
This gives us two possible solutions:
x₁ = (1 + 23) / 44 = 24/44 = 6/11
x₂ = (1 - 23) / 44 = -22/44 = -1/2
-
Check for extraneous solutions and ensure lengths are positive:
Let's check x₁ = 6/11:
PQ = 3(6/11) - 14 = -136/11 (negative) QR = 7(6/11) - 10 = -68/11 (negative) AC = 4(6/11) + 2 = 46/11 (positive) DF = 2(6/11) + 1 = 23/11 (positive)
Since PQ and QR are negative, x₁ = 6/11 is not a valid solution.
Now let's check x₂ = -1/2:
PQ = 3(-1/2) - 14 = -3/2 - 28/2 = -31/2 (negative)
QR = 7(-1/2) - 10 = -7/2 - 20/2 = -27/2 (negative)
AC = 4(-1/2) + 2 = -2 + 2 = 0 (zero length, also problematic)
DF = 2(-1/2) + 1 = -1 + 1 = 0 (zero length, also problematic)
Since PQ and QR are negative and AC and DF are zero, x₂ = -1/2 is also not a valid solution. In this case, it strongly suggests that the initial problem setup is flawed or intentionally designed to demonstrate the importance of verifying solutions in a geometric context. It's highly probable that the given expressions or relationships are incorrect, leading to these non-sensical outcomes.
General Steps for Solving for 'x'
Here's a summary of the general steps to follow when solving for 'x' in these types of problems:
- Understand the Given Information: Carefully read the problem statement and identify the relationships between the line segments (congruence, collinearity, ratio, similarity, etc.). Draw a diagram if necessary.
- Set up an Equation: Translate the geometric relationship into an algebraic equation using the given expressions for the lengths of the line segments.
- Solve for 'x': Use algebraic techniques to isolate 'x' and find its value. This might involve:
- Combining like terms
- Distributing
- Solving linear equations
- Solving quadratic equations (using factoring, the quadratic formula, or completing the square)
- Check Your Solution: Crucially, substitute the value of 'x' back into the original expressions for the lengths of the line segments.
- Verify that the lengths are positive. Lengths cannot be negative in standard Euclidean geometry. If you obtain a negative length, it indicates an error in the problem statement, the assumed relationships, or your calculations. The problem might be deliberately designed to highlight this issue.
- Verify that the solution satisfies the initial geometric relationships. For example, if you assumed PQ = QR, make sure that the calculated lengths of PQ and QR are indeed equal.
The Importance of Context and Verification
The examples above demonstrate a crucial point: simply solving an equation for 'x' is not enough. You must interpret the solution in the context of the geometric problem. In many cases, algebraic manipulation will yield a numerical value for 'x', but that value might not be a valid solution to the geometric problem because it leads to negative lengths or violates other geometric principles.
Always remember to:
- Check for negative lengths.
- Verify that the solution satisfies the initial geometric conditions.
- If a solution doesn't make sense geometrically, revisit the problem statement and your assumptions. There might be a subtle error in the problem or a misunderstanding of the relationships between the segments.
- Consider the possibility that the problem is deliberately designed to illustrate the importance of verifying solutions.
Common Mistakes to Avoid
- Forgetting to distribute: When an expression is multiplied by a factor (e.g., 2(7x - 10)), make sure to distribute the factor to both terms inside the parentheses.
- Combining unlike terms: Only combine terms that have the same variable and exponent (e.g., 3x and 7x can be combined, but 3x and 7x² cannot).
- Incorrectly applying the order of operations: Remember PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction).
- Ignoring negative signs: Pay close attention to negative signs when manipulating equations. A misplaced negative sign can lead to an incorrect solution.
- Failing to check your solution: Always plug the value of 'x' back into the original expressions to verify that it makes sense in the context of the problem.
- Not considering the geometric implications of the solution: Remember that lengths cannot be negative, and solutions must be consistent with the given geometric relationships.
Conclusion
Solving for 'x' in expressions like PQ 3x-14 and QR 7x-10 requires a combination of algebraic skills and geometric understanding. By carefully analyzing the relationships between the line segments, setting up appropriate equations, solving for 'x', and most importantly, verifying the solution in the context of the geometric problem, you can successfully tackle these types of challenges. Always remember that algebra is a tool, and the ultimate goal is to solve a geometric problem, not just to find a numerical value for 'x'. The geometric context will always be the final arbiter of whether a solution is valid.
Latest Posts
Latest Posts
-
What Can Management Researchers Infer Based On This Study
Nov 03, 2025
-
What Is The Missing Value In The Table Below
Nov 03, 2025
-
An Important Feature Of Emergency Operation Plans Is That They
Nov 03, 2025
-
Complete The Following Table With Information About Each Chemical Tested
Nov 03, 2025
-
Which Of The Following Solutions Is Basic
Nov 03, 2025
Related Post
Thank you for visiting our website which covers about Pq 3x 14 And Qr 7x 10 Find X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.