Pr 9x 31 And Qr 43 Find X
arrobajuarez
Dec 06, 2025 · 8 min read
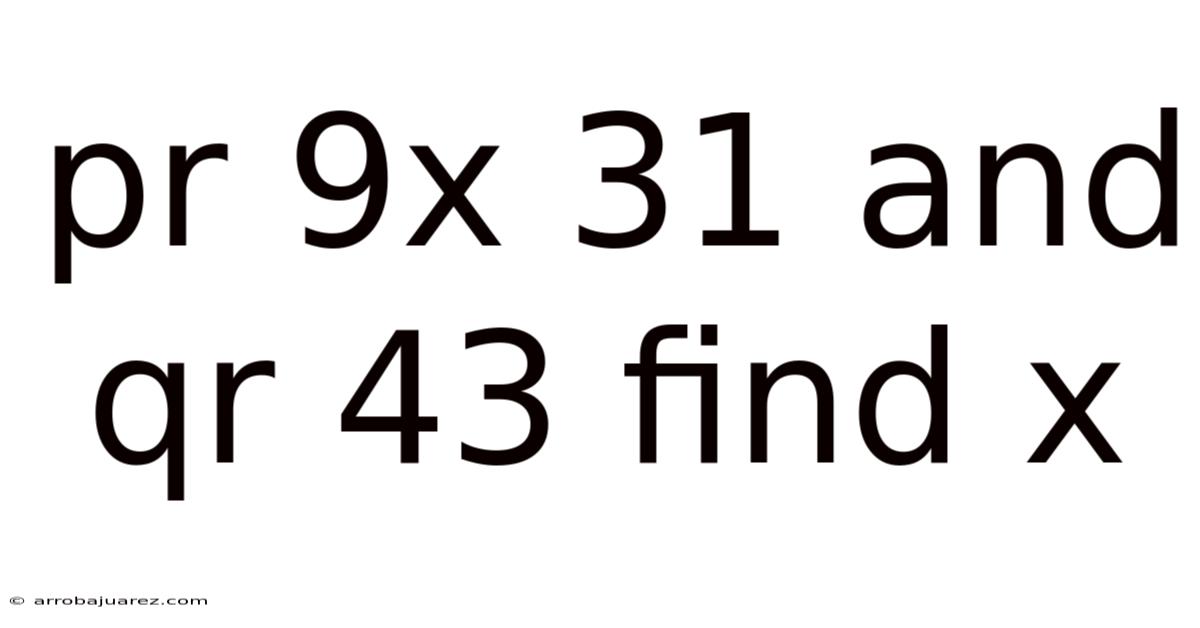
Table of Contents
Alright, let's dive into solving algebraic problems involving ratios and proportions, specifically tackling problems of the type "PR 9x/31 and QR 43/find x." This type of problem requires a deep understanding of proportionality, cross-multiplication, and sometimes, algebraic manipulation. We’ll break down the concepts, methodologies, and provide examples to ensure a comprehensive understanding.
Understanding Ratios and Proportions
Before diving into the specifics of solving "PR 9x/31 and QR 43/find x" type problems, it's crucial to have a solid grasp of what ratios and proportions are.
A ratio is a comparison of two quantities, often expressed as a fraction. For example, if there are 9 apples and 31 oranges, the ratio of apples to oranges is 9:31 or 9/31.
A proportion is a statement that two ratios are equal. For instance, if the ratio of apples to oranges in one basket is the same as in another basket, we can set up a proportion.
Key Concepts:
- Ratio: A comparison of two quantities.
- Proportion: An equation stating that two ratios are equal.
- Cross-Multiplication: A method used to solve proportions by multiplying the numerator of one ratio by the denominator of the other and setting the products equal.
Breaking Down the Problem: "PR 9x/31 and QR 43/find x"
The problem "PR 9x/31 and QR 43/find x" presents a scenario where we have two ratios: 9x/31 and 43/x. The goal is to find the value of 'x' that makes these ratios proportional or related in a specific way. The 'PR' and 'QR' likely indicate some relationship or context, which might involve further constraints or equations.
Setting Up the Proportion
The fundamental step is to recognize that we're dealing with a proportion. If we assume that the problem implies these two ratios are equal, we can set up the equation:
9x/31 = 43/x
Solving for x using Cross-Multiplication
To solve for x, we use the method of cross-multiplication. This involves multiplying the numerator of the first fraction by the denominator of the second fraction and vice versa, then setting these products equal to each other:
(9x) * (x) = 43 * 31
This simplifies to:
9x² = 1333
Isolating x²
Next, we isolate x² by dividing both sides of the equation by 9:
x² = 1333 / 9
x² ≈ 148.11
Finding x
To find x, we take the square root of both sides of the equation:
x = √148.11
x ≈ ±12.17
Therefore, x is approximately 12.17 or -12.17. The context of the problem might dictate whether we accept both solutions or only the positive one (e.g., if x represents a physical quantity, a negative value might not be applicable).
Advanced Scenarios and Considerations
While the basic approach involves direct proportionality, many problems are more complex. Let’s consider some variations and how to approach them.
Inverse Proportionality
Sometimes, the problem might imply an inverse relationship between the ratios. In this case, the product of corresponding terms is constant, rather than the ratios being equal.
If 9x/31 and 43/x are inversely proportional, then:
(9x) * (43) = 31 * x
387x = 31x
This simplifies to:
387x - 31x = 0
356x = 0
x = 0
In an inverse proportion context, x would be 0. However, this result should be checked against the original problem statement to ensure it is a valid solution.
Introducing Additional Variables and Constraints
Real-world problems often include additional variables and constraints. For example:
PR = 9x/31 and QR = 43/x, where PR + QR = 25
In this case, we have an additional equation that relates PR and QR. We can substitute the expressions for PR and QR into the equation:
(9x/31) + (43/x) = 25
To solve this, we first eliminate the fractions by multiplying every term by 31x:
31x * (9x/31) + 31x * (43/x) = 25 * 31x
This simplifies to:
9x² + 1333 = 775x
Rearranging the terms gives us a quadratic equation:
9x² - 775x + 1333 = 0
Solving the Quadratic Equation
To solve the quadratic equation 9x² - 775x + 1333 = 0, we can use the quadratic formula:
x = [-b ± √(b² - 4ac)] / (2a)
Where a = 9, b = -775, and c = 1333.
x = [775 ± √((-775)² - 4 * 9 * 1333)] / (2 * 9)
x = [775 ± √(600625 - 47988)] / 18
x = [775 ± √552637] / 18
x = [775 ± 743.4] / 18
This gives us two possible values for x:
x₁ = (775 + 743.4) / 18 ≈ 84.36
x₂ = (775 - 743.4) / 18 ≈ 1.76
Both values should be checked in the context of the original problem to ensure they are valid.
Practical Examples
Let’s consider a few practical examples to illustrate how these concepts are applied.
Example 1: Scaling Recipes
Suppose a recipe requires flour and sugar in the ratio of 9x grams of flour to 31 grams of sugar. If you want to scale the recipe such that you use 43 grams of sugar, how much flour (x) do you need?
Here, PR represents the amount of flour and QR represents the amount of sugar.
The proportion is:
9x/31 = 43/x
Cross-multiplying gives:
9x² = 43 * 31
9x² = 1333
x² = 1333 / 9
x² ≈ 148.11
x ≈ √148.11
x ≈ 12.17
So, you would need approximately 9 * 12.17 = 109.53 grams of flour.
Example 2: Map Distances
On a map, the ratio of the distance between two cities is represented as 9x cm to 31 cm. If the actual distance between another pair of cities is 43 km and represented on the map by x cm, find the value of x.
Here, PR and QR represent the scale factors for different distances.
The proportion is:
9x/31 = 43/x
Cross-multiplying gives:
9x² = 43 * 31
9x² = 1333
x² = 1333 / 9
x² ≈ 148.11
x ≈ √148.11
x ≈ 12.17
So, x ≈ 12.17 cm represents 43 km on the map.
Example 3: Chemical Concentrations
In a chemical solution, the ratio of two compounds is 9x units to 31 units. If you want to maintain a proportional mixture where the second compound is 43 units, and x represents the adjustment factor, find x.
The proportion is:
9x/31 = 43/x
Cross-multiplying gives:
9x² = 43 * 31
9x² = 1333
x² = 1333 / 9
x² ≈ 148.11
x ≈ √148.11
x ≈ 12.17
So, the adjustment factor x is approximately 12.17.
Common Pitfalls and How to Avoid Them
When solving proportion problems, several common pitfalls can lead to incorrect answers. Here’s how to avoid them:
- Incorrectly Setting Up the Proportion: Ensure that corresponding quantities are placed in the correct positions in the ratios. For example, if you are comparing apples to oranges, make sure apples are always in the numerator or always in the denominator.
- Forgetting to Consider Units: If the quantities are in different units, convert them to the same unit before setting up the proportion.
- Misapplying Cross-Multiplication: Double-check that you are multiplying the correct terms when cross-multiplying.
- Ignoring Context: Always consider the context of the problem. Negative values or zero values might not make sense in certain situations.
- Algebraic Errors: Be careful with algebraic manipulations, especially when dealing with quadratic equations.
Conclusion
Solving problems of the type "PR 9x/31 and QR 43/find x" involves understanding ratios, proportions, and algebraic manipulation. By correctly setting up the proportion, using cross-multiplication, and considering any additional constraints or relationships, you can find the value of x. Whether dealing with direct or inverse proportionality, or more complex equations, a systematic approach will help ensure accurate results. Remember to always check your answers against the context of the problem to ensure they make sense. Understanding these principles will equip you to tackle a wide range of problems involving ratios and proportions effectively.
Frequently Asked Questions (FAQ)
Q: What does PR and QR mean in the context of the problem?
A: PR and QR likely denote specific quantities or conditions related to the ratios. They could represent labels for the ratios, constraints, or variables that further define the problem. The exact meaning depends on the specific problem statement.
Q: Can x be negative in these types of problems?
A: Yes, x can be negative, but it depends on the context of the problem. If x represents a physical quantity that cannot be negative (e.g., distance, mass), then only the positive solution is valid.
Q: What if the ratios are inversely proportional?
A: If the ratios are inversely proportional, the product of corresponding terms is constant. Set up the equation as (9x) * (43) = 31 * x and solve for x.
Q: How do I handle problems with additional constraints or equations?
A: Substitute the given ratios into the additional equations and solve the resulting system of equations. This might involve solving quadratic equations or other algebraic manipulations.
Q: Is cross-multiplication always the best method to solve proportions?
A: Cross-multiplication is a convenient method for solving proportions, but it's essential to understand the underlying principles. For more complex problems, algebraic manipulation might be necessary to isolate x.
Q: What should I do if I get a quadratic equation when solving for x?
A: Use the quadratic formula to find the values of x. Be sure to check both solutions in the context of the original problem to determine if both are valid.
Q: How do I check my answer?
A: Substitute the value of x back into the original proportion or equations. Verify that the ratios are equal or that the equations are satisfied.
By mastering these concepts and practicing with different examples, you'll be well-prepared to tackle any problem involving ratios and proportions.
Latest Posts
Related Post
Thank you for visiting our website which covers about Pr 9x 31 And Qr 43 Find X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.