3 X 2 5 X 2
arrobajuarez
Oct 27, 2025 · 10 min read
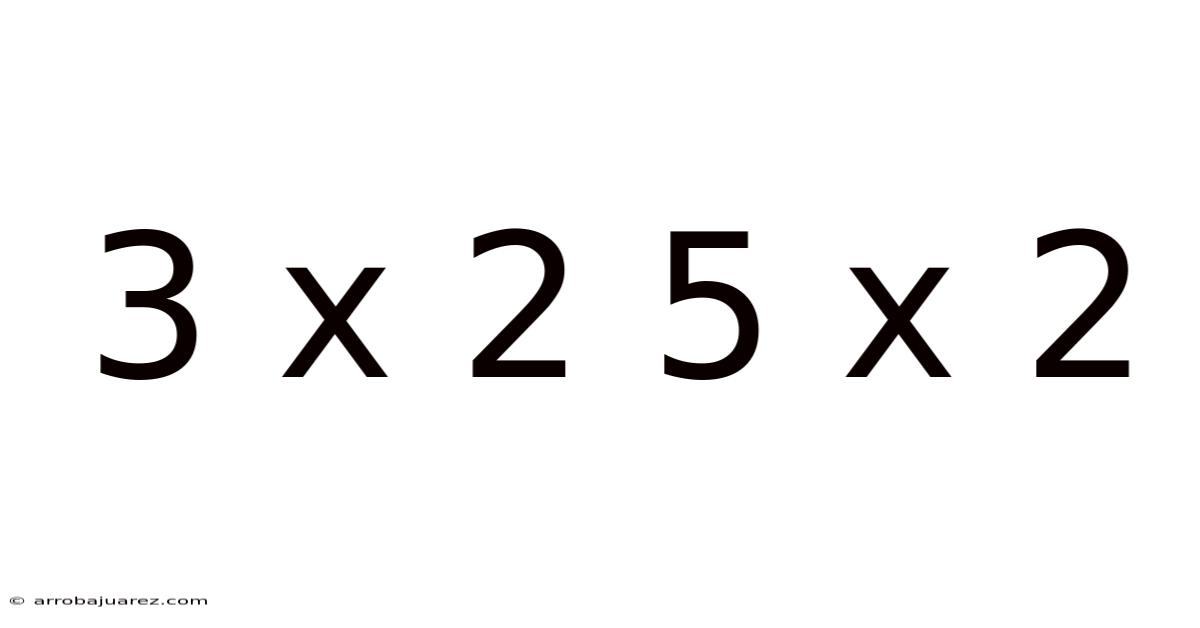
Table of Contents
Exploring the Nuances of 3 x 2 and 5 x 2: A Comprehensive Guide
Mathematical expressions like 3 x 2 and 5 x 2 appear simple on the surface, but they represent fundamental concepts in arithmetic. Understanding these concepts provides a solid foundation for more complex mathematical operations. This article will delve into the meaning of these expressions, explore different methods of solving them, and discuss their real-world applications. We'll also touch upon the underlying mathematical principles that make these calculations so important.
The Basics: Understanding Multiplication
Before diving into the specifics of 3 x 2 and 5 x 2, it's essential to understand the basic principle of multiplication. Multiplication is a mathematical operation that represents repeated addition. In simpler terms, it's a shortcut for adding the same number multiple times.
- Multiplier: The number that indicates how many times the other number is added.
- Multiplicand: The number being multiplied.
- Product: The result of the multiplication.
For instance, in the expression 3 x 2, '3' is the multiplier and '2' is the multiplicand. The product is the result we obtain after performing the multiplication.
Demystifying 3 x 2: Three Groups of Two
The expression 3 x 2 means "three groups of two." Imagine you have three separate containers, and each container holds two apples. To find the total number of apples, you would add the number of apples in each container together: 2 + 2 + 2.
Methods to Solve 3 x 2:
- Repeated Addition: As mentioned earlier, 3 x 2 is equivalent to 2 + 2 + 2. Adding these numbers together gives us 6.
- Number Line: You can visualize this on a number line. Start at 0, then make three jumps of 2 units each. You will land on the number 6.
- Visual Representation: Draw three circles, and inside each circle, draw two dots. Count all the dots, and you'll find there are six dots in total.
- Memorization: Ideally, memorizing basic multiplication facts is the quickest method. Knowing that 3 x 2 equals 6 allows for instant recall.
Real-World Applications of 3 x 2:
- Baking: If a recipe calls for 2 cups of flour per cake and you want to bake 3 cakes, you'll need 3 x 2 = 6 cups of flour.
- Cost Calculation: If each candy bar costs $2 and you want to buy 3 candy bars, the total cost will be 3 x $2 = $6.
- Arranging Objects: Imagine you have 3 rows of chairs, with 2 chairs in each row. You have a total of 3 x 2 = 6 chairs.
Exploring 5 x 2: Five Groups of Two
The expression 5 x 2 signifies "five groups of two." Picture having five bags, each containing two marbles. To determine the total number of marbles, you would add the number of marbles in each bag: 2 + 2 + 2 + 2 + 2.
Methods to Solve 5 x 2:
- Repeated Addition: 5 x 2 is equivalent to 2 + 2 + 2 + 2 + 2. Adding these numbers together results in 10.
- Number Line: Begin at 0 on a number line and make five jumps of 2 units each. You will arrive at the number 10.
- Visual Representation: Draw five squares, and inside each square, draw two small squares. Count all the small squares; you'll find there are ten in total.
- Memorization: Similar to 3 x 2, memorizing the multiplication fact that 5 x 2 equals 10 is the most efficient method.
Real-World Applications of 5 x 2:
- Sharing: If you have 5 friends and you want to give each friend 2 cookies, you'll need 5 x 2 = 10 cookies.
- Time Management: If you spend 2 hours per day studying for 5 days a week, you spend a total of 5 x 2 = 10 hours studying.
- Construction: If you need 5 pieces of wood, each 2 feet long, you require a total of 5 x 2 = 10 feet of wood.
The Commutative Property of Multiplication
A crucial concept to understand is the commutative property of multiplication. This property states that the order of the numbers being multiplied does not affect the product. In mathematical terms:
a x b = b x a
Therefore, 3 x 2 is the same as 2 x 3, and 5 x 2 is the same as 2 x 5.
- 2 x 3: This means "two groups of three." Imagine two containers, each holding three apples. The total number of apples is 3 + 3 = 6.
- 2 x 5: This means "two groups of five." Imagine two bags, each containing five marbles. The total number of marbles is 5 + 5 = 10.
Understanding this property can simplify problem-solving and provide a deeper understanding of how multiplication works.
Multiplication Tables: Building a Foundation
Multiplication tables are essential tools for mastering basic multiplication facts. Familiarizing yourself with the multiplication tables for 2, 3, and 5 will significantly improve your speed and accuracy in performing calculations.
-
The 2 Times Table: This table is relatively easy to learn as it simply involves doubling numbers.
- 2 x 1 = 2
- 2 x 2 = 4
- 2 x 3 = 6
- 2 x 4 = 8
- 2 x 5 = 10
- 2 x 6 = 12
- 2 x 7 = 14
- 2 x 8 = 16
- 2 x 9 = 18
- 2 x 10 = 20
-
The 3 Times Table: This table builds on the 2 times table and introduces a slightly more complex pattern.
- 3 x 1 = 3
- 3 x 2 = 6
- 3 x 3 = 9
- 3 x 4 = 12
- 3 x 5 = 15
- 3 x 6 = 18
- 3 x 7 = 21
- 3 x 8 = 24
- 3 x 9 = 27
- 3 x 10 = 30
-
The 5 Times Table: This table is often the easiest to learn because the products always end in either 0 or 5.
- 5 x 1 = 5
- 5 x 2 = 10
- 5 x 3 = 15
- 5 x 4 = 20
- 5 x 5 = 25
- 5 x 6 = 30
- 5 x 7 = 35
- 5 x 8 = 40
- 5 x 9 = 45
- 5 x 10 = 50
Regular practice with these tables will solidify your understanding of multiplication and make solving problems like 3 x 2 and 5 x 2 automatic.
The Associative Property of Multiplication
While the commutative property deals with the order of two numbers, the associative property of multiplication deals with grouping three or more numbers. This property states that the way numbers are grouped in a multiplication problem does not change the result. In mathematical terms:
(a x b) x c = a x (b x c)
Although this property is more relevant when dealing with three or more numbers, understanding it can provide a more complete picture of how multiplication works.
Distributive Property of Multiplication
The distributive property of multiplication combines multiplication with addition or subtraction. It states that multiplying a number by a sum or difference is the same as multiplying the number by each term in the sum or difference and then adding or subtracting the results. In mathematical terms:
a x (b + c) = (a x b) + (a x c)
a x (b - c) = (a x b) - (a x c)
While not directly applicable to simple expressions like 3 x 2 or 5 x 2, understanding this property is crucial for solving more complex algebraic problems.
Expanding on the Basics: Multiplication with Larger Numbers
The principles used to solve 3 x 2 and 5 x 2 can be extended to multiplication with larger numbers. For example, consider the problem 3 x 25.
Methods to Solve 3 x 25:
- Repeated Addition: 3 x 25 is equivalent to 25 + 25 + 25. Adding these numbers together gives us 75.
- Breaking Down the Number: You can break down 25 into 20 + 5. Then, use the distributive property: 3 x (20 + 5) = (3 x 20) + (3 x 5) = 60 + 15 = 75.
- Standard Multiplication Algorithm: This is the traditional method taught in schools, involving multiplying each digit of the multiplicand by the multiplier and then adding the results.
Similarly, consider the problem 5 x 12.
Methods to Solve 5 x 12:
- Repeated Addition: 5 x 12 is equivalent to 12 + 12 + 12 + 12 + 12. Adding these numbers together gives us 60.
- Breaking Down the Number: You can break down 12 into 10 + 2. Then, use the distributive property: 5 x (10 + 2) = (5 x 10) + (5 x 2) = 50 + 10 = 60.
- Standard Multiplication Algorithm: Again, this involves multiplying each digit of the multiplicand by the multiplier and adding the results.
Common Mistakes and How to Avoid Them
Even with simple multiplication problems, it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
- Misunderstanding the Operation: Confusing multiplication with addition or subtraction is a common mistake, especially among young learners. Reinforce the concept that multiplication is repeated addition.
- Skipping Steps: When using repeated addition, ensure you add the number the correct number of times. Double-check your work to avoid errors.
- Memorization Errors: Relying solely on memorization without understanding the underlying concept can lead to mistakes. Make sure you understand why 3 x 2 = 6 and not some other number.
- Careless Calculation: Simple addition errors can lead to incorrect answers. Take your time and double-check your calculations.
Multiplication and Division: Inverse Operations
Multiplication and division are inverse operations. This means that one operation undoes the other. Understanding this relationship can help you solve problems more efficiently and check your answers.
- 3 x 2 = 6 implies that 6 ÷ 2 = 3 and 6 ÷ 3 = 2.
- 5 x 2 = 10 implies that 10 ÷ 2 = 5 and 10 ÷ 5 = 2.
This relationship can be used to verify your multiplication results. For example, if you calculate that 3 x 2 = 7, you can quickly check your answer by dividing 7 by 2 or 3. If the result is not a whole number, you know you've made a mistake.
Multiplication in Different Contexts
Multiplication is not just a mathematical operation; it's a fundamental concept that appears in various contexts.
- Geometry: Calculating the area of a rectangle involves multiplication. The area of a rectangle with a length of 5 units and a width of 2 units is 5 x 2 = 10 square units.
- Computer Science: Multiplication is used extensively in computer programming for tasks such as calculating memory addresses, scaling images, and performing complex simulations.
- Finance: Calculating interest, determining investment returns, and budgeting all rely on multiplication.
The Importance of Practice
Like any skill, mastering multiplication requires consistent practice. Here are some tips for practicing multiplication:
- Use Flashcards: Create flashcards with multiplication problems on one side and the answers on the other. Practice with these flashcards regularly to improve your recall speed.
- Online Resources: Numerous websites and apps offer interactive multiplication games and exercises. These resources can make learning fun and engaging.
- Real-World Problems: Apply multiplication to real-world scenarios. For example, calculate the cost of buying multiple items, determine the amount of ingredients needed for a recipe, or estimate travel time based on speed and distance.
- Worksheets: Practice with multiplication worksheets to reinforce your understanding of the concepts and improve your accuracy.
Conclusion: Building Blocks for Mathematical Success
Understanding simple multiplication problems like 3 x 2 and 5 x 2 forms the foundation for more advanced mathematical concepts. By mastering these basics, you build a solid base for tackling more complex calculations, algebraic equations, and real-world problem-solving. This article has explored the meaning of these expressions, presented various methods for solving them, and discussed their practical applications. Remember, consistent practice and a solid understanding of the underlying principles are key to achieving mathematical success. From repeated addition to the commutative property, each concept contributes to a deeper appreciation of the power and versatility of multiplication.
Latest Posts
Latest Posts
-
How Do I Merge Cells In Excel
Oct 27, 2025
-
Procedure 1 Tracing Substances Through The Kidney
Oct 27, 2025
-
Which Of The Following Correctly Describes Nims
Oct 27, 2025
-
Diffusion Is Directional Non Random Passive None Of The Above
Oct 27, 2025
-
Which Of The Following Statements About Catalysts Is False
Oct 27, 2025
Related Post
Thank you for visiting our website which covers about 3 X 2 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.