What Is The Value Of X 75 37
arrobajuarez
Nov 22, 2025 · 7 min read
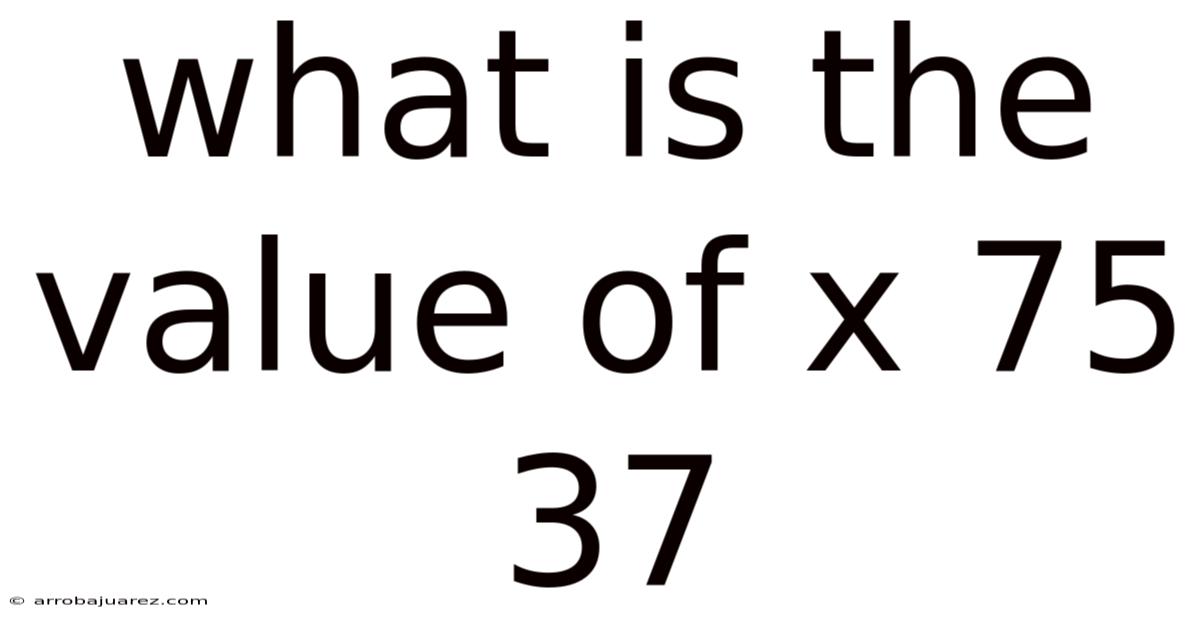
Table of Contents
The quest to decipher the value of 'x' in the enigmatic expression "x 75 37" is a journey into the realm of mathematical ambiguity and the subtle art of interpretation. The value of 'x' is highly dependent on the context, the intended operations, and the assumptions we make about the expression's underlying structure.
Decoding the Enigma: Interpreting "x 75 37"
The expression "x 75 37" presents a tantalizing puzzle because it lacks explicit operators and clear instructions. To unravel its meaning, we must explore the potential scenarios and mathematical interpretations that could give 'x' a definitive value.
Scenario 1: 'x' as a Variable in an Incomplete Equation
-
Interpretation: 'x' represents an unknown variable in an unfinished equation where "75 37" is part of a larger expression.
-
Explanation: Without an equation to solve, the value of 'x' remains undetermined. We need an equation that includes "x 75 37" to find 'x'.
- Example: If the equation is x + 75 = 37, then x = 37 - 75 = -38.
Scenario 2: 'x' as a Multiplication Factor
-
Interpretation: The expression implies multiplication between 'x' and the number formed by '7537'.
-
Explanation: If we treat "75 37" as the number 7537, the expression becomes a simple multiplication:
- x * 7537 = y (where 'y' is the result)
- The value of 'x' depends on what the expression is equal to. For example, if x * 7537 = 15074, then x = 15074 / 7537 = 2.
Scenario 3: 'x' as a Digit in a Number Sequence
-
Interpretation: 'x' is a digit that, when combined with 75 and 37, forms a numerical sequence.
-
Explanation: The expression "x 75 37" could be part of a larger numerical sequence. In this case, 'x' would be a digit that fits into the sequence according to a defined pattern.
- Example: If the sequence is based on odd numbers, then x = 1 would make the sequence 1, 75, 37 (though this sequence doesn't follow a clear arithmetic pattern).
Scenario 4: 'x' as a Function Argument
-
Interpretation: 'x' is an argument to a function applied to the numbers 75 and 37.
-
Explanation: This implies a function f(x, 75, 37) where 'x' influences the result along with the constants 75 and 37.
- Example: If f(x, 75, 37) = x * (75 - 37), then f(x, 75, 37) = x * 38. Without knowing the value of the function, 'x' remains undefined.
Scenario 5: 'x' in Modular Arithmetic
-
Interpretation: The expression involves modular arithmetic operations with 'x', 75, and 37.
-
Explanation: Modular arithmetic deals with remainders. We might be looking at an expression like (x + 75) mod 37 = y.
- To find 'x', we would need to know the value of 'y' or the specific modular relationship.
Scenario 6: 'x' as a Coordinate
-
Interpretation: In a coordinate system, 'x' could be one coordinate, with 75 and 37 possibly representing other coordinates or parameters.
-
Explanation: In a 3D space, we might have a point (x, 75, 37). Without further context, 'x' can be any real number.
Scenario 7: 'x' in a Matrix or Vector Context
-
Interpretation: 'x' could be an element in a matrix or vector that includes 75 and 37.
-
Explanation: For example, we might have a vector [x, 75, 37]. Again, without additional context, 'x' is unconstrained.
The Need for Context
Without additional information, the value of 'x' in "x 75 37" is inherently ambiguous. Context is crucial to understanding the relationship between 'x', 75, and 37. Here are the types of context that would be helpful:
- Equation: Is "x 75 37" part of an equation? If so, what is the equation?
- Function: Is there a function that takes 'x', 75, and 37 as inputs?
- Sequence: Is "x 75 37" part of a numerical sequence?
- Mathematical Operation: What operations (addition, subtraction, multiplication, division, modular arithmetic, etc.) are involved?
- Domain: What is the domain of 'x'? Is 'x' an integer, a real number, or something else?
Mathematical Manipulations and Scenarios
To illustrate how the value of 'x' can be determined under different conditions, let's consider some examples:
Example 1: Simple Linear Equation
Assume "x 75 37" is part of the equation:
x + 75 = 37
To solve for 'x':
x = 37 - 75 x = -38
In this case, x = -38.
Example 2: Multiplication and Division
Assume "x 75 37" is part of the equation:
x * 75 = 37
To solve for 'x':
x = 37 / 75 x ≈ 0.4933
In this case, x ≈ 0.4933.
Example 3: A More Complex Equation
Assume "x 75 37" is part of the equation:
x^2 + 75 = 37 * x
Rearrange the equation:
x^2 - 37x + 75 = 0
This is a quadratic equation. To solve for 'x', we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
Where a = 1, b = -37, and c = 75.
x = (37 ± √((-37)^2 - 4 * 1 * 75)) / (2 * 1) x = (37 ± √(1369 - 300)) / 2 x = (37 ± √1069) / 2 x = (37 ± 32.695) / 2
So, we have two possible values for 'x':
x1 = (37 + 32.695) / 2 ≈ 34.8475 x2 = (37 - 32.695) / 2 ≈ 2.1525
In this case, x ≈ 34.8475 or x ≈ 2.1525.
Example 4: Modular Arithmetic
Assume the expression is part of a modular equation:
(x + 75) mod 37 = 0
This means (x + 75) is divisible by 37. So:
x + 75 = 37 * k (where k is an integer)
x = 37 * k - 75
If k = 2:
x = 37 * 2 - 75 x = 74 - 75 x = -1
If k = 3:
x = 37 * 3 - 75 x = 111 - 75 x = 36
In general, x = 37k - 75, where k is an integer.
Example 5: Function Definition
Assume we define a function:
f(x, a, b) = x * a + b
Then, in our case:
f(x, 75, 37) = x * 75 + 37
If we want to find 'x' such that f(x, 75, 37) = 0:
x * 75 + 37 = 0 x * 75 = -37 x = -37 / 75 x ≈ -0.4933
In this case, x ≈ -0.4933.
Example 6: Sequence Pattern
Let's try to find a pattern in the sequence x, 75, 37. Suppose it's an arithmetic sequence.
75 - x = 37 - 75 75 - x = -38 x = 75 + 38 x = 113
However, this doesn't seem to follow an obvious pattern. Let's consider a geometric sequence:
75 / x = 37 / 75 37x = 75 * 75 37x = 5625 x = 5625 / 37 x ≈ 152.027
Without a clearly defined pattern, it's hard to determine 'x' precisely in a sequence.
Common Pitfalls
When attempting to find the value of 'x' in ambiguous expressions, watch out for:
- Assuming Implicit Operations: Automatically assuming multiplication or addition without explicit operators can lead to incorrect results.
- Ignoring Context: Failing to consider the context in which the expression appears.
- Overlooking Multiple Solutions: Some equations have multiple solutions, and it's important to find all possible values for 'x'.
- Arithmetic Errors: Careless mistakes in calculations can lead to wrong answers.
- Misinterpreting Mathematical Notation: Ensure a solid understanding of mathematical notation to avoid misinterpreting the expression.
The Importance of Clear Mathematical Notation
The ambiguity of the expression "x 75 37" underscores the importance of clear and unambiguous mathematical notation. In mathematical communication, precision is essential to avoid misunderstandings.
- Use of Operators: Always explicitly indicate mathematical operations using symbols like +, -, *, /, etc.
- Parentheses: Use parentheses to group terms and clarify the order of operations.
- Functions: Clearly define any functions used, including their inputs and outputs.
- Context: Provide sufficient context to avoid ambiguity.
Conclusion
In conclusion, the value of 'x' in the expression "x 75 37" cannot be definitively determined without additional context or information. The expression is ambiguous and open to multiple interpretations. Depending on the assumed context—whether it's part of an equation, a function, a sequence, or a different mathematical structure—the value of 'x' can vary widely. Therefore, clear mathematical notation and sufficient context are crucial to avoid ambiguity and ensure accurate communication. The puzzle of "x 75 37" serves as a reminder of the subtle yet significant role that context plays in mathematical problem-solving.
Latest Posts
Latest Posts
-
Calculate Cash Flow To Creditors For Fy24
Nov 22, 2025
-
When Computing Wacc An Analyst Should Use The
Nov 22, 2025
-
For A Purely Competitive Seller Price Equals
Nov 22, 2025
-
Deconstruct The Given Diels Alder Adduct
Nov 22, 2025
-
What Is The Value Of X 75 37
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 75 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.