X 1 X 2 X 1
arrobajuarez
Nov 22, 2025 · 12 min read
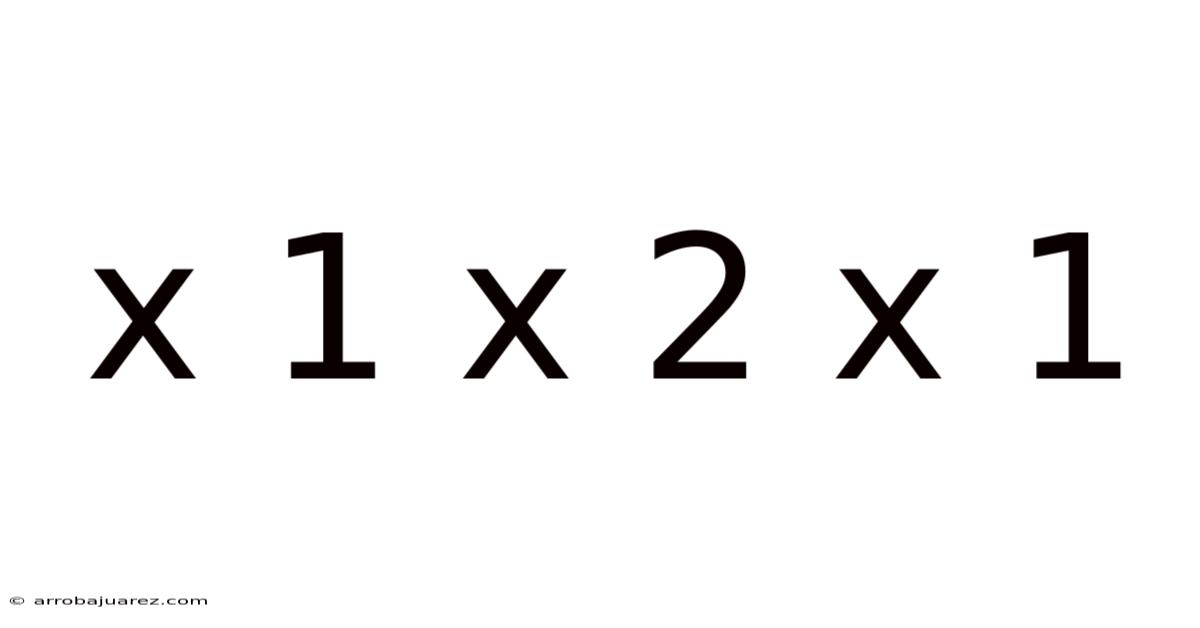
Table of Contents
Understanding the "x 1 x 2 x 1" Pattern: A Comprehensive Guide
The "x 1 x 2 x 1" pattern, while seemingly abstract, represents a powerful concept applicable across various fields, from mathematics and computer science to music and design. It signifies a sequence of actions, elements, or values where a starting point (x) is followed by a single iteration of one process (1), then a doubled or amplified iteration of another process (2), and finally, a return to a single iteration of the initial process (1). Understanding this pattern requires dissecting its components and exploring its diverse applications. This article aims to provide a comprehensive understanding of the "x 1 x 2 x 1" pattern, delving into its underlying principles, practical examples, and potential implications.
Unpacking the Core Components
Before diving into specific applications, it's crucial to define the individual components of the "x 1 x 2 x 1" pattern:
- x: Represents the initial condition, starting point, or the foundational element. This can be a number, a variable, a musical note, a color, or any definable entity. It acts as the anchor for the subsequent operations. The nature of 'x' dictates the context and the meaning of the entire pattern.
- 1: Signifies a single, standard, or basic operation or iteration. It's the first action performed on or in relation to 'x.' It can be an addition, a multiplication, a transformation, or a simple repetition. This '1' represents a unit of change or progress.
- 2: Represents a doubled, amplified, or intensified version of a different operation or process. This is the point where the pattern introduces a significant change or acceleration. It contrasts with the single iteration represented by '1,' creating a sense of dynamic movement. The '2' can represent a multiplication by two, a doubling of effort, or a combination of two elements.
- 1 (again): This final '1' signifies a return to the initial type of operation or process, mirroring the first '1.' It creates a sense of closure and symmetry within the pattern. This return can represent a correction, a completion, or a stabilization of the process.
The "x 1 x 2 x 1" pattern, therefore, describes a sequence that starts with a base element, undergoes a single change, experiences a significant amplification or alteration, and then returns to a state of equilibrium or completion related to the initial change.
Applications in Mathematics
The "x 1 x 2 x 1" pattern manifests in various mathematical concepts and operations. Let's examine a few examples:
-
Basic Arithmetic: Consider 'x' as a number. Let '1' be the addition of a constant 'a,' and '2' be the multiplication by a constant 'b.' The pattern then translates to:
x + a, (x + a) * b * 2, (x + a) * b * 2 + a. This demonstrates how the pattern can represent a sequence of arithmetic operations.- For instance, if x = 5, a = 2, and b = 3, the sequence becomes: 5 + 2 = 7, 7 * 3 * 2 = 42, 42 + 2 = 44.
-
Algebraic Equations: The pattern can be observed in simplifying or solving equations. Consider an equation where 'x' is a variable. The '1' could represent adding a term to both sides, '2' could represent multiplying both sides by a constant, and the final '1' could represent subtracting another term to isolate 'x.'
-
Sequences and Series: The pattern can define the structure of a specific sequence. For example, the terms of a sequence might follow the rule derived from the pattern, where each term is calculated based on the previous term and the "x 1 x 2 x 1" operations.
-
Calculus (Derivatives and Integrals): In simplified scenarios, 'x' could be a function. '1' could represent taking the first derivative, '2' could represent taking the second derivative (or multiplying the first derivative by a constant), and the final '1' could represent integrating the second derivative to obtain a function related to the original. This illustrates how the pattern can loosely represent operations in calculus, although direct application might be more complex.
Applications in Computer Science
The "x 1 x 2 x 1" pattern is particularly relevant in computer science, especially in algorithms and data structures:
-
Algorithm Design: Many algorithms follow a general structure that aligns with this pattern.
-
Initialization (x): Setting up the initial state of the data or variables.
-
Single Step (1): Performing a basic operation on the data (e.g., comparing two elements, incrementing a counter).
-
Amplified Processing (2): Executing a more complex or resource-intensive operation (e.g., sorting a subset of data, searching for a specific element). This often involves looping or recursion.
-
Final Adjustment (1): Performing a final adjustment or cleanup step to ensure the algorithm's correctness and efficiency (e.g., merging sorted subsets, verifying the result).
-
Example: A simplified sorting algorithm. 'x' is the unsorted list. The first '1' could be finding the minimum element. The '2' could be moving that minimum element to its correct position (which might involve multiple swaps). The final '1' would be incrementing the index to repeat the process for the remaining unsorted portion of the list.
-
-
Data Structures: The pattern can be used in designing and manipulating data structures.
- Linked Lists: 'x' is the head node. The first '1' is traversing to the next node. '2' could be inserting a new node (which involves updating pointers of two nodes). The final '1' could be traversing to the subsequent node after the insertion.
- Binary Trees: 'x' is the root node. The first '1' is traversing to the left child. '2' could be processing the node (e.g., printing its value) and then traversing to the right child. The final '1' is returning to the parent node.
-
Software Development Lifecycle: A simplified view of software development can be seen through the "x 1 x 2 x 1" lens.
- Planning (x): Initial project definition and scope.
- Basic Coding (1): Implementing core functionalities.
- Testing and Debugging (2): Identifying and fixing errors, which often requires significantly more effort than initial coding.
- Refinement and Deployment (1): Optimizing code and releasing the software.
-
Machine Learning: While more complex, the pattern can be loosely applied to some machine learning processes.
- Initialization (x): Setting initial weights and biases in a neural network.
- Forward Pass (1): Calculating the output based on the input and current weights.
- Backpropagation (2): Calculating the gradients and updating the weights, often involving more complex computations than the forward pass. This '2' represents a larger and more impactful change.
- Evaluation (1): Assessing the model's performance and making minor adjustments (e.g., learning rate).
Applications in Music
The "x 1 x 2 x 1" pattern finds resonance in musical composition and structure:
- Melodic Structure: 'x' could represent a starting note or chord. The first '1' could be a step-wise movement to the next note. The '2' could be a leap to a note further away, creating a more dramatic interval. The final '1' could be a step back towards the original starting note, creating a sense of resolution.
- Rhythmic Patterns: 'x' could represent a rhythmic unit (e.g., a quarter note). The first '1' could be a single repetition of that unit. The '2' could be a doubling of the rhythmic unit (e.g., two quarter notes tied together, or a half note). The final '1' could be a return to the single rhythmic unit. This creates a rhythmic variation and a sense of rhythmic completeness.
- Harmonic Progressions: 'x' could represent the tonic chord (I). The first '1' could be moving to the subdominant chord (IV). The '2' could be a strong progression to the dominant chord (V), which often creates tension. The final '1' could be resolving back to the tonic chord (I), providing a sense of harmonic closure. This I-IV-V-I (altered) progression is a foundational element in many musical styles. This '2' represents the intensified pull towards resolution.
- Song Structure (Verse-Chorus): While not a direct application, the verse-chorus structure can be loosely interpreted. 'x' is the introduction. '1' is the verse. '2' is the chorus (which is often more emphasized and repeated). The final '1' is another verse before potentially leading to a bridge or outro.
Applications in Design
The principles of the "x 1 x 2 x 1" pattern can be applied to various design disciplines, including graphic design, web design, and user interface (UI) design:
- Visual Hierarchy: 'x' could represent a primary element (e.g., a logo). The first '1' could be a supporting element (e.g., a heading). The '2' could be a dominant element (e.g., a large image or a call-to-action button), drawing the user's attention. The final '1' could be another supporting element, creating a balanced and visually appealing composition. The '2' is deliberately emphasized to guide the user's eye.
- Color Palette: 'x' could be a base color. The first '1' could be a complementary color. The '2' could be an accent color that is used sparingly but effectively to draw attention to specific elements. The final '1' could be a neutral color that provides balance and contrast. The '2' adds visual interest and excitement.
- UI Design (User Flow): 'x' is the initial landing page. The first '1' is a simple action (e.g., clicking a link). The '2' is a more significant action (e.g., completing a form or making a purchase), representing the core purpose of the user's interaction. The final '1' is a confirmation or thank-you page, providing feedback to the user. The '2' is the conversion point.
- Web Layout: 'x' is the header. The first '1' is the navigation bar. '2' is the main content area, which occupies the most prominent space. The final '1' is the footer.
Abstract and Conceptual Applications
Beyond concrete examples, the "x 1 x 2 x 1" pattern can also represent more abstract concepts:
- Problem Solving: 'x' is the initial problem statement. The first '1' is identifying the root cause. The '2' is brainstorming and implementing potential solutions, which may require significant effort and creativity. The final '1' is evaluating the effectiveness of the solution.
- Learning Process: 'x' is the initial exposure to a new concept. The first '1' is basic understanding and memorization. The '2' is applying the concept to complex problems and real-world scenarios, which requires deeper understanding and critical thinking. The final '1' is reinforcing the understanding through practice and reflection.
- Personal Growth: 'x' is the current state. The first '1' is identifying a desired change. The '2' is taking significant action to achieve that change, which may involve challenges and setbacks. The final '1' is integrating the change into one's life and maintaining the progress.
- Project Management: 'x' is the project kickoff. '1' is the initial task assignment. '2' is the execution phase, where multiple tasks are completed concurrently. The final '1' is the final review and handover.
Limitations and Considerations
While the "x 1 x 2 x 1" pattern provides a useful framework for understanding sequences and processes, it's important to acknowledge its limitations:
- Oversimplification: The pattern is a simplified representation of reality and may not fully capture the complexity of real-world scenarios. Many processes involve multiple iterations, feedback loops, and non-linear relationships that are not easily represented by this pattern.
- Context Dependence: The meaning of "x," "1," and "2" is highly context-dependent. Without a clear understanding of the context, the pattern can be misinterpreted or misapplied.
- Not a Universal Rule: Not all processes or sequences follow this pattern. It is a useful tool for analysis and design, but it should not be considered a universal rule.
- Subjectivity: The interpretation of "amplification" or "intensification" (represented by "2") can be subjective. What constitutes a significant change in one context may be insignificant in another.
Frequently Asked Questions (FAQ)
- Is the "x 1 x 2 x 1" pattern a mathematical formula? No, it is not a strict mathematical formula. It is more of a conceptual framework or a sequence that can be applied in various fields. The actual mathematical operations represented by "1" and "2" will depend on the specific context.
- Where does the "x 1 x 2 x 1" pattern originate from? There is no single origin point. It's a pattern that has emerged independently in various disciplines as a way to describe and understand sequences of events or actions. Its simplicity and versatility make it a recurring theme.
- How can I use the "x 1 x 2 x 1" pattern in my work? Start by identifying the key components of the process or sequence you are analyzing. Define what "x," "1," and "2" represent in that context. Then, consider how the pattern can help you understand the structure, identify potential bottlenecks, or design improvements.
- Is the "x 1 x 2 x 1" pattern related to any specific mathematical or scientific theory? Not directly, but it shares similarities with concepts like feedback loops, iterative processes, and harmonic progressions. It is a general pattern that can be applied to a wide range of phenomena.
- Can the "x 1 x 2 x 1" pattern be extended? Yes, the pattern can be extended or modified to accommodate more complex scenarios. For example, you could add more iterations or introduce nested patterns. The key is to maintain a clear understanding of the underlying principles.
Conclusion
The "x 1 x 2 x 1" pattern, despite its simplicity, offers a powerful lens through which to analyze and understand sequences and processes across diverse fields. From mathematics and computer science to music and design, the pattern highlights the importance of a starting point, a single iteration, an amplified action, and a return to a state of equilibrium. While not a universal rule, it provides a valuable framework for problem-solving, design thinking, and understanding the underlying structure of complex systems. By recognizing and applying this pattern, we can gain deeper insights and develop more effective strategies in various aspects of our lives and work. The key takeaway is to appreciate the pattern's adaptability and use it as a tool to simplify and understand the world around us. Remember to define the elements precisely within the context you're working, and the 'x 1 x 2 x 1' pattern can be a surprisingly versatile problem-solving and analytical technique.
Latest Posts
Latest Posts
-
The One Fixed Asset That Is Not Depreciated Is
Nov 22, 2025
-
Person Centered Care Means All Of The Following Except
Nov 22, 2025
-
X 1 X 2 X 1
Nov 22, 2025
-
The Description Is Progressively Throughout The Project
Nov 22, 2025
-
Which Piecewise Relation Defines A Function
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about X 1 X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.