X 2 2 4 Y 1
arrobajuarez
Nov 19, 2025 · 9 min read
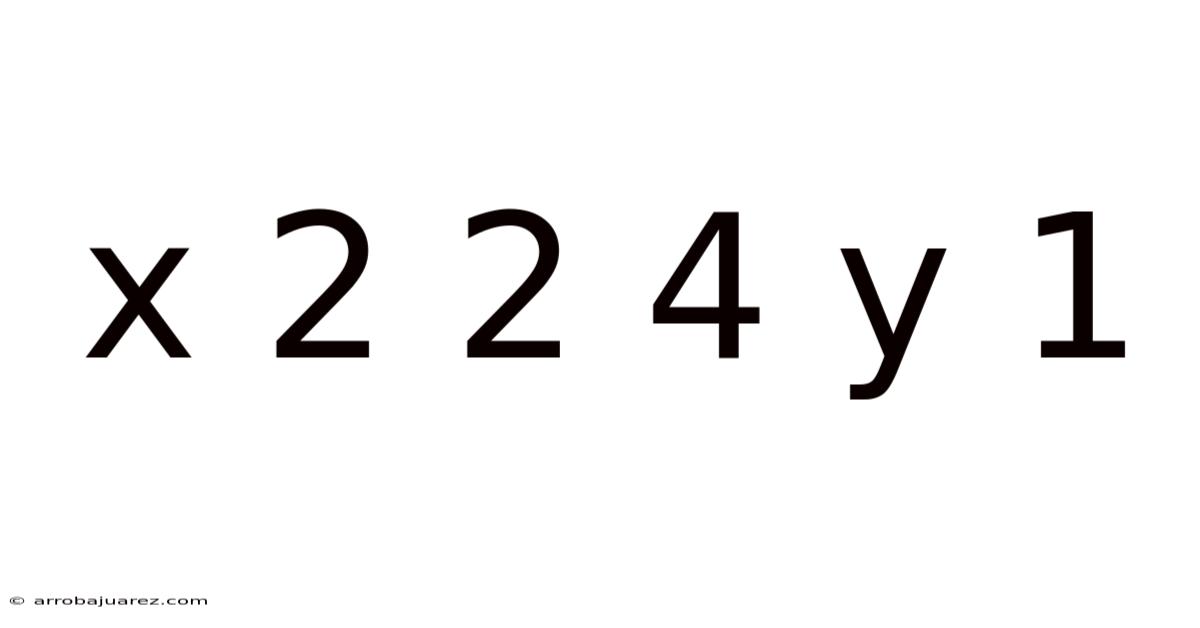
Table of Contents
Exploring the Depths of the Equation: x² + 2² = 4y + 1
In mathematics, even the simplest-looking equations can unveil a world of intriguing properties and connections. The equation x² + 2² = 4y + 1, with its blend of quadratic and linear terms, is a prime example. This equation, seemingly straightforward, opens the door to exploring number theory, algebraic manipulation, and the fascinating relationships between variables.
A Deep Dive into the Equation
Let's begin by dissecting the equation itself. We have x², a quadratic term representing the square of the variable x. Then, we have 2², which is simply the constant 4. On the other side of the equation, we encounter 4y, a linear term representing four times the variable y, and finally, the constant 1.
The challenge lies in understanding the constraints and properties that emerge when these terms interact. What values can x and y take? Are there patterns or relationships between them? These are the questions we'll explore.
Rewriting the Equation for Clarity
To gain a better understanding, we can rewrite the equation slightly:
x² + 4 = 4y + 1
Subtracting 1 from both sides, we get:
x² + 3 = 4y
Now, we can isolate y:
y = (x² + 3) / 4
This form is incredibly useful because it directly expresses y in terms of x. For any chosen value of x, we can immediately calculate the corresponding value of y. However, there's a crucial constraint: y must be an integer. This means that (x² + 3) must be divisible by 4. This divisibility requirement introduces a new layer of complexity and structure to our exploration.
Integer Solutions: The Key to Unlocking the Equation
The requirement that y must be an integer significantly restricts the possible values of x. Let's investigate this further. For (x² + 3) to be divisible by 4, x² + 3 must be a multiple of 4. In other words:
x² + 3 ≡ 0 (mod 4)
This is a modular arithmetic expression, which means that x² + 3 leaves a remainder of 0 when divided by 4. We can rearrange this to:
x² ≡ -3 (mod 4)
Since -3 is congruent to 1 modulo 4, we can further simplify:
x² ≡ 1 (mod 4)
This congruence tells us that x² must leave a remainder of 1 when divided by 4. Let's examine the possible remainders when a number is squared and then divided by 4.
Analyzing Possible Values of x Modulo 4
Consider the possible remainders when x is divided by 4: 0, 1, 2, and 3.
- If x ≡ 0 (mod 4), then x² ≡ 0² ≡ 0 (mod 4)
- If x ≡ 1 (mod 4), then x² ≡ 1² ≡ 1 (mod 4)
- If x ≡ 2 (mod 4), then x² ≡ 2² ≡ 4 ≡ 0 (mod 4)
- If x ≡ 3 (mod 4), then x² ≡ 3² ≡ 9 ≡ 1 (mod 4)
From this analysis, we see that x² can only be congruent to 0 or 1 modulo 4. Our requirement is that x² ≡ 1 (mod 4). This means that x must be congruent to either 1 or 3 modulo 4. In simpler terms, x must be an odd number.
Finding Integer Solutions: A Systematic Approach
Now that we know x must be odd, we can express x in the form 2k + 1, where k is an integer. Substituting this into our equation for y:
y = ((2k + 1)² + 3) / 4
Expanding the square:
y = (4k² + 4k + 1 + 3) / 4
y = (4k² + 4k + 4) / 4
Factoring out a 4:
y = 4(k² + k + 1) / 4
Finally, we get:
y = k² + k + 1
This equation tells us that for any integer value of k, we can find corresponding integer values for x and y that satisfy our original equation. Specifically, x = 2k + 1 and y = k² + k + 1.
Generating Solutions: Examples
Let's generate some solutions by choosing different values for k:
-
If k = 0, then x = 2(0) + 1 = 1, and y = 0² + 0 + 1 = 1. So, (x, y) = (1, 1) is a solution. Let's check: 1² + 4 = 5 and 4(1) + 1 = 5. Correct!
-
If k = 1, then x = 2(1) + 1 = 3, and y = 1² + 1 + 1 = 3. So, (x, y) = (3, 3) is a solution. Let's check: 3² + 4 = 13 and 4(3) + 1 = 13. Correct!
-
If k = 2, then x = 2(2) + 1 = 5, and y = 2² + 2 + 1 = 7. So, (x, y) = (5, 7) is a solution. Let's check: 5² + 4 = 29 and 4(7) + 1 = 29. Correct!
-
If k = 3, then x = 2(3) + 1 = 7, and y = 3² + 3 + 1 = 13. So, (x, y) = (7, 13) is a solution. Let's check: 7² + 4 = 53 and 4(13) + 1 = 53. Correct!
We can continue generating solutions indefinitely by choosing different integer values for k.
The Nature of the Solutions: A Parabolic Relationship
The equation y = k² + k + 1 reveals a significant property of the solutions. It represents a parabola. This means that the values of y increase quadratically as k (and therefore x) increases. The solutions (x, y) are not linearly related; the y values grow much faster than the x values.
We can also express y directly in terms of x. Since x = 2k + 1, then k = (x - 1) / 2. Substituting this into the equation for y:
y = ((x - 1) / 2)² + ((x - 1) / 2) + 1
y = (x² - 2x + 1) / 4 + (x - 1) / 2 + 1
Multiplying the second term by 2/2 to get a common denominator:
y = (x² - 2x + 1) / 4 + (2x - 2) / 4 + 4/4
Combining the terms:
y = (x² - 2x + 1 + 2x - 2 + 4) / 4
y = (x² + 3) / 4
This is the same equation we derived earlier, confirming the consistency of our approach.
Exploring Variations and Related Equations
What happens if we change the constants in the original equation? For example, consider x² + a² = by + c, where a, b, and c are integers. The approach to solving this equation is similar:
- Rewrite the equation to isolate y: y = (x² + a² - c) / b
- For y to be an integer, (x² + a² - c) must be divisible by b.
- Analyze the possible values of x modulo b.
- Find a general form for x that guarantees an integer value for y.
- Express y in terms of a new integer variable (like our k).
The specific details will change depending on the values of a, b, and c, but the overall strategy remains the same. The key is to use modular arithmetic to understand the divisibility constraints and then find a parametric representation for the solutions.
Computational Verification: Using Code to Find Solutions
We can write a simple Python script to verify our solutions and generate more examples:
def find_solutions(limit):
"""Finds integer solutions for x² + 4 = 4y + 1 where x and y are less than the limit."""
solutions = []
for k in range(limit):
x = 2*k + 1
y = k**2 + k + 1
if x**2 + 4 == 4*y + 1:
solutions.append((x, y))
return solutions
# Find solutions where x and y are less than 100
solutions = find_solutions(100)
# Print the solutions
for x, y in solutions:
print(f"x = {x}, y = {y}")
This code iterates through values of k, calculates x and y, and then verifies that they satisfy the original equation. It prints out all solutions where both x and y are less than 100. This provides a computational check on our analytical results.
The Importance of Constraints
The equation x² + 2² = 4y + 1 demonstrates the crucial role of constraints in mathematical problem-solving. The requirement that y must be an integer dramatically narrows down the possible values of x. Without this constraint, we would have an infinite number of real-number solutions.
This idea is fundamental to many areas of mathematics and computer science. Constraints define the boundaries of a problem and guide us towards meaningful solutions. In optimization problems, for example, constraints specify the feasible region, the set of solutions that satisfy certain conditions.
Beyond the Basics: Connecting to Number Theory
This equation touches on several concepts in number theory:
-
Diophantine Equations: These are equations where we seek integer solutions. Our equation is a simple example of a Diophantine equation.
-
Modular Arithmetic: We used modular arithmetic to analyze the divisibility requirements and understand the possible values of x modulo 4.
-
Quadratic Residues: The concept of quadratic residues is related to finding solutions to congruences of the form x² ≡ a (mod m). Our analysis of x² ≡ 1 (mod 4) is an example of this.
Further exploration into these areas would provide a deeper understanding of the properties and solutions of equations like x² + 2² = 4y + 1.
Real-World Applications (Indirectly)
While this specific equation might not have direct, obvious real-world applications, the mathematical principles involved are widely used:
-
Cryptography: Number theory, including modular arithmetic and Diophantine equations, is essential for modern cryptography.
-
Computer Science: Algorithms for solving equations and optimizing solutions are fundamental to computer science.
-
Engineering: Mathematical modeling and equation solving are used extensively in engineering to design and analyze systems.
The Power of Algebraic Manipulation
Throughout our exploration, we've relied heavily on algebraic manipulation. Rewriting the equation, isolating variables, and substituting expressions are all crucial techniques for understanding and solving mathematical problems. These skills are essential for anyone studying mathematics, science, or engineering.
Limitations and Further Research
While we've found a general solution for the equation, there are still some avenues for further research:
-
Generalizations: Can we find a general solution for equations of the form x² + a² = by + c, where a, b, and c are integers?
-
Other Constraints: What happens if we impose additional constraints on x and y, such as requiring them to be positive or prime numbers?
-
Geometric Interpretation: Is there a geometric interpretation of the solutions to this equation?
Conclusion: A Journey Through a Simple Equation
The equation x² + 2² = 4y + 1, though seemingly simple, has provided a rich and insightful journey into the world of mathematics. We've explored algebraic manipulation, modular arithmetic, and the importance of constraints. We've found a general solution, generated examples, and connected the equation to broader concepts in number theory. This exploration highlights the power of mathematics to reveal hidden structures and relationships, even in the most unassuming equations. The key takeaway is that by carefully analyzing the equation and applying the right techniques, we can unlock its secrets and gain a deeper appreciation for the beauty and elegance of mathematics. From its humble beginnings, the equation has led us through a landscape of concepts, demonstrating the interconnectedness of mathematical ideas.
Latest Posts
Latest Posts
-
A Response Strategy Requires Suppliers Be Selected Based Primarily On
Nov 20, 2025
-
1 1 1 1 In Binary
Nov 20, 2025
-
You Need To Design A 60 0 Hz Ac Generator
Nov 20, 2025
-
Which Histograms Shown Below Are Skewed To The Left
Nov 20, 2025
-
Corina Is Outgoing Warm And Truly Inspirational
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 2 4 Y 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.