Y 2 X 2 2z 2
arrobajuarez
Nov 09, 2025 · 11 min read
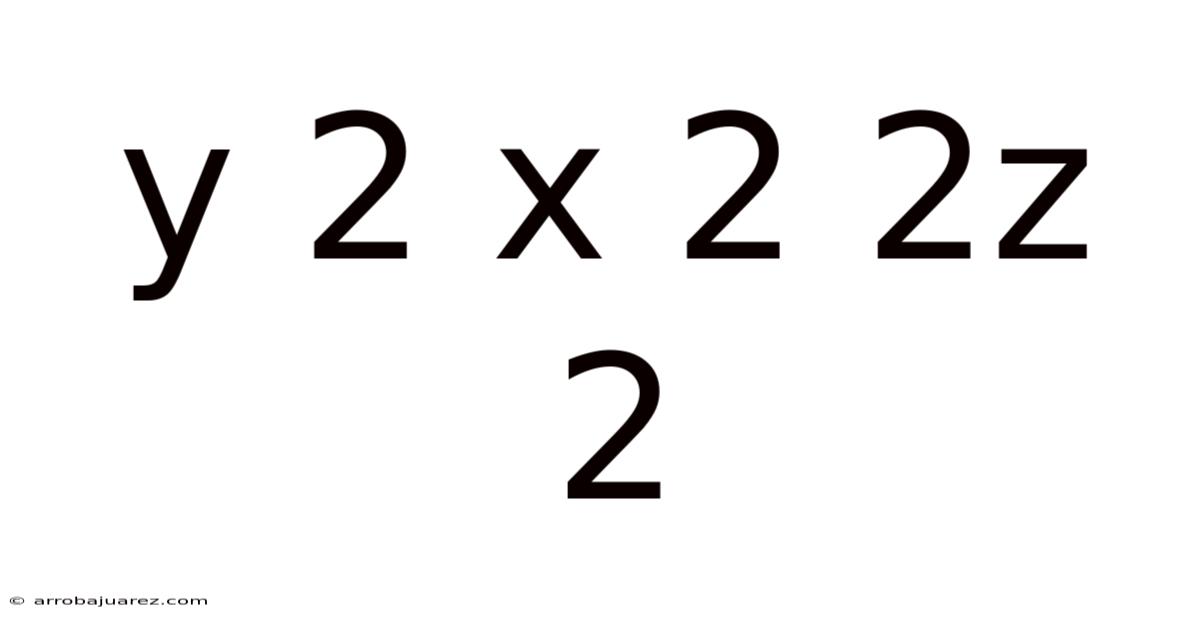
Table of Contents
Navigating the landscape of algebraic expressions can sometimes feel like deciphering a complex code. One such expression that often pops up in mathematical discussions is "y^2 - x^2 - 2z^2". This seemingly simple arrangement of variables and coefficients holds a wealth of mathematical properties and applications. Understanding this expression, its variations, and its implications is crucial for anyone delving into algebra, calculus, or related fields.
Unpacking the Basics: What Does y^2 - x^2 - 2z^2 Mean?
At its core, "y^2 - x^2 - 2z^2" is a polynomial expression involving three variables: x, y, and z. Each variable is raised to the power of 2, indicating a quadratic term. The expression combines these terms through subtraction and multiplication by a constant.
Here's a breakdown:
- y^2: This term represents the square of the variable y. It signifies y multiplied by itself (y * y).
- x^2: Similarly, this term represents the square of the variable x (x * x).
- 2z^2: This term represents twice the square of the variable z. It signifies 2 multiplied by z squared (2 * z * z).
The expression as a whole describes a relationship between these squared terms. The subtraction operations imply that the value of y squared is being reduced by the values of x squared and twice z squared.
Diving Deeper: Exploring the Significance of y^2 - x^2 - 2z^2
While the expression itself might seem abstract, its significance becomes apparent when considering its applications and relationships to other mathematical concepts.
- Geometric Representation: In three-dimensional space, expressions involving squared terms often relate to geometric shapes. The expression "y^2 - x^2 - 2z^2 = k" (where k is a constant) represents a quadric surface. Specifically, it's a hyperboloid. The specific shape depends on the value of k.
- Conic Sections: When we fix one of the variables (e.g., setting z to a constant), the expression can reduce to a conic section in the remaining two variables. For example, if z = 0, we have y^2 - x^2 = k, which is the equation of a hyperbola.
- Quadratic Forms: The expression is a quadratic form, which is a homogeneous polynomial of degree two. Quadratic forms are fundamental in linear algebra and have applications in optimization, physics, and other areas.
Step-by-Step Guide: Working with the Expression y^2 - x^2 - 2z^2
Let's delve into some practical ways to manipulate and work with the expression "y^2 - x^2 - 2z^2".
1. Evaluating the Expression for Given Values:
The most straightforward task is evaluating the expression when given specific values for x, y, and z.
Example: Let's say x = 2, y = 5, and z = 1.
- Substitute the values: (5)^2 - (2)^2 - 2(1)^2
- Calculate the squares: 25 - 4 - 2(1)
- Multiply: 25 - 4 - 2
- Subtract: 21 - 2 = 19
Therefore, when x = 2, y = 5, and z = 1, the value of the expression y^2 - x^2 - 2z^2 is 19.
2. Factoring (When Possible):
While the expression "y^2 - x^2 - 2z^2" doesn't have a simple, direct factorization, we can explore some possibilities:
- Difference of Squares (Partial): We can group the first two terms: (y^2 - x^2) - 2z^2. The term (y^2 - x^2) is a difference of squares and can be factored as (y + x)(y - x). So, the expression becomes: (y + x)(y - x) - 2z^2. This doesn't lead to a complete factorization but can be useful in some contexts.
- No Simple General Factorization: In general, there isn't a simple, closed-form factorization for the entire expression "y^2 - x^2 - 2z^2" over real numbers.
3. Solving for One Variable in Terms of Others:
We can rearrange the expression to solve for one variable in terms of the others. For example, let's solve for y:
- Start with: y^2 - x^2 - 2z^2 = 0 (Setting the expression equal to zero for simplicity)
- Add x^2 and 2z^2 to both sides: y^2 = x^2 + 2z^2
- Take the square root of both sides: y = ±√(x^2 + 2z^2)
This gives us y as a function of x and z.
Similarly, we can solve for x or z. For example, solving for x:
- Start with: y^2 - x^2 - 2z^2 = 0
- Add x^2 to both sides: y^2 - 2z^2 = x^2
- Take the square root of both sides: x = ±√(y^2 - 2z^2)
And solving for z:
- Start with: y^2 - x^2 - 2z^2 = 0
- Add 2z^2 to both sides: y^2 - x^2 = 2z^2
- Divide by 2: (y^2 - x^2)/2 = z^2
- Take the square root of both sides: z = ±√((y^2 - x^2)/2)
4. Completing the Square (With Modifications):
While directly completing the square isn't applicable to the entire expression in a simple way, we can manipulate it for specific purposes. For instance, if we're trying to analyze the expression in relation to a particular variable, completing the square (or a modified version of it) might be useful.
Real-World Applications and Examples
While the expression "y^2 - x^2 - 2z^2" might seem theoretical, it has connections to various real-world applications, often indirectly through related mathematical concepts.
- Physics (Relativity): In the context of special relativity, similar expressions appear in the calculation of spacetime intervals. While the exact form might differ (e.g., involving the speed of light), the concept of subtracting squared terms relates to the geometry of spacetime.
- Engineering (Structural Analysis): Quadric surfaces, which are represented by equations involving squared terms like those in our expression, are used in the design and analysis of structures such as bridges and buildings. Understanding the properties of these surfaces is crucial for ensuring stability and load-bearing capacity.
- Computer Graphics (3D Modeling): Quadric surfaces are also used in computer graphics for modeling 3D objects. While more complex surfaces are often used, understanding the basics of quadric surfaces provides a foundation for creating and manipulating 3D shapes.
- Optimization Problems: Quadratic forms, of which our expression is an example, are used extensively in optimization problems. These problems involve finding the maximum or minimum value of a function subject to certain constraints. Quadratic forms arise in various applications, such as portfolio optimization in finance and control systems in engineering.
Understanding Related Mathematical Concepts
To fully grasp the expression "y^2 - x^2 - 2z^2", it's helpful to understand some related mathematical concepts:
- Polynomials: The expression is a polynomial in three variables. Understanding the properties of polynomials, such as degree, coefficients, and roots, is essential.
- Quadratic Forms: As mentioned earlier, the expression is a quadratic form. Studying linear algebra and matrix theory will provide a deeper understanding of quadratic forms and their properties.
- Conic Sections: Understanding conic sections (circles, ellipses, parabolas, hyperbolas) provides a geometric intuition for expressions involving squared terms.
- Quadric Surfaces: Expanding on conic sections, quadric surfaces are the three-dimensional analogs of conic sections. Studying their properties will help visualize and understand the geometric representation of the expression.
- Linear Algebra: Linear algebra provides the tools for analyzing quadratic forms, understanding their transformations, and finding their eigenvalues and eigenvectors.
- Calculus: Calculus is used to find the extrema (maximum or minimum values) of functions involving expressions like "y^2 - x^2 - 2z^2".
Common Mistakes and How to Avoid Them
When working with expressions like "y^2 - x^2 - 2z^2", it's easy to make mistakes. Here are some common pitfalls and how to avoid them:
- Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS). Exponents (squaring) should be performed before multiplication and subtraction.
- Sign Errors: Be careful with negative signs. Remember that subtracting a negative number is the same as adding a positive number. Also, pay attention to the signs when solving for variables.
- Incorrectly Applying the Difference of Squares: The difference of squares factorization (a^2 - b^2 = (a + b)(a - b)) only applies to the difference of two squares. Don't try to apply it to expressions that don't fit this form.
- Forgetting the ± Sign When Taking Square Roots: When solving for a variable by taking the square root, remember to include both the positive and negative roots. For example, if x^2 = 9, then x = ±3.
- Algebraic Errors: Double-check your algebra when manipulating the expression. Make sure you're applying the rules of algebra correctly.
- Misinterpreting the Geometry: When relating the expression to geometric shapes, be careful to correctly identify the type of conic section or quadric surface.
Advanced Concepts and Extensions
For those interested in delving deeper, here are some advanced concepts and extensions related to the expression "y^2 - x^2 - 2z^2":
- Diagonalization of Quadratic Forms: In linear algebra, a key technique is to diagonalize a quadratic form. This involves finding a change of variables that transforms the quadratic form into a simpler expression involving only squared terms without cross-product terms.
- Sylvester's Law of Inertia: This theorem states that the number of positive, negative, and zero eigenvalues of a quadratic form is invariant under a change of basis. This is a fundamental result in the theory of quadratic forms.
- Definite and Indefinite Quadratic Forms: Quadratic forms can be classified as positive definite, negative definite, positive semi-definite, negative semi-definite, or indefinite, based on the signs of their eigenvalues. This classification has important implications in optimization and stability analysis.
- Applications in Optimization: Quadratic forms are used in optimization problems to model the objective function or the constraints. Understanding the properties of quadratic forms is essential for designing efficient optimization algorithms.
- Relationship to Eigenvalues and Eigenvectors: The eigenvalues and eigenvectors of the matrix associated with a quadratic form provide valuable information about the shape and orientation of the corresponding quadric surface.
- Tensor Analysis: In more advanced contexts, quadratic forms can be generalized to tensors. Tensor analysis is used in physics and engineering to describe physical quantities that transform in a specific way under coordinate transformations.
Examples of Problem-Solving with y^2 - x^2 - 2z^2
Let's explore some example problems that involve the expression "y^2 - x^2 - 2z^2":
Problem 1:
Given that y^2 - x^2 - 2z^2 = 5, and x = 1, z = 2, find the value of y.
Solution:
- Substitute the given values into the equation: y^2 - (1)^2 - 2(2)^2 = 5
- Simplify: y^2 - 1 - 8 = 5
- Combine like terms: y^2 - 9 = 5
- Add 9 to both sides: y^2 = 14
- Take the square root of both sides: y = ±√14
Therefore, the values of y are √14 and -√14.
Problem 2:
Describe the geometric shape represented by the equation y^2 - x^2 - 2z^2 = 0.
Solution:
The equation y^2 - x^2 - 2z^2 = 0 represents a cone in three-dimensional space. This can be seen by rearranging the equation as y^2 = x^2 + 2z^2. This equation is a homogeneous equation of degree 2, which is characteristic of a cone.
Problem 3:
Find the values of x, y, and z that satisfy the equation y^2 - x^2 - 2z^2 = 0, subject to the constraints x = z and y > 0.
Solution:
- Substitute x = z into the equation: y^2 - z^2 - 2z^2 = 0
- Simplify: y^2 - 3z^2 = 0
- Rearrange: y^2 = 3z^2
- Take the square root of both sides: y = ±√(3z^2) = ±z√3
Since y > 0, we have y = z√3.
Therefore, the solutions are of the form (x, y, z) = (z, z√3, z), where z can be any real number.
Problem 4:
Determine if the quadratic form represented by y^2 - x^2 - 2z^2 is positive definite, negative definite, or indefinite.
Solution:
The quadratic form is indefinite. This can be determined by examining the coefficients of the squared terms. Since the coefficient of y^2 is positive (+1) and the coefficients of x^2 and z^2 are negative (-1 and -2, respectively), the quadratic form can take both positive and negative values depending on the values of x, y, and z. For example:
- If x = 0, y = 1, z = 0, then y^2 - x^2 - 2z^2 = 1 > 0.
- If x = 2, y = 0, z = 0, then y^2 - x^2 - 2z^2 = -4 < 0.
Since the quadratic form can take both positive and negative values, it is indefinite.
Conclusion
The expression "y^2 - x^2 - 2z^2" serves as a gateway to understanding a range of mathematical concepts, from basic algebraic manipulation to advanced topics in linear algebra and geometry. By exploring its properties, applications, and relationships to other concepts, one can gain a deeper appreciation for the interconnectedness of mathematics and its relevance to the real world. While it might seem like just a collection of variables and coefficients, this expression unlocks a world of mathematical insights and problem-solving opportunities.
Latest Posts
Latest Posts
-
Reaction Rates And Chemical Equilibrium Lab Answers
Nov 09, 2025
-
Two Customers Purchased The Same Kind Of Bread
Nov 09, 2025
-
A Policy Of Adhesion Can Only Be Modified By Whom
Nov 09, 2025
-
Remove The Panes From The Worksheet
Nov 09, 2025
-
Elaine Wakes Up In The Hospital With A Head Injury
Nov 09, 2025
Related Post
Thank you for visiting our website which covers about Y 2 X 2 2z 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.